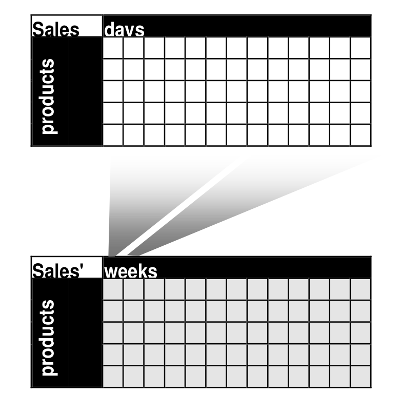
4. Query Language Guide

4.1. Preface

4.1.1. Overview

This guide provides information about how to use the rasdaman database management system (in short: rasdaman). The document explains usage of the rasdaman Query Language.

Follow the instructions in this guide as you develop your application which makes use of rasdaman services. Explanations detail how to create type definitions and instances; how to retrieve information from databases; how to insert, manipulate, and delete instances within databases.

4.1.2. Audience

The information in this manual is intended primarily for application developers; additionally, it can be useful for advanced users of rasdaman applications and for database administrators.

4.1.3. Rasdaman Documentation Set

This manual should be read in conjunction with the complete rasdaman documentation set which this guide is part of. The documentation set in its completeness covers all important information needed to work with the rasdaman system, such as programming and query access to databases, guidance to utilities such as raswct, release notes, and additional information on the rasdaman wiki.

4.2. Introduction

4.2.1. Multidimensional Data

In principle, any natural phenomenon becomes spatio-temporal array data of some specific dimensionality once it is sampled and quantised for storage and manipulation in a computer system; additionally, a variety of artificial sources such as simulators, image renderers, and data warehouse population tools generate array data. The common characteristic they all share is that a large set of large multidimensional arrays has to be maintained. We call such arrays multidimensional discrete data (or short: MDD) expressing the variety of dimensions and separating them from the conceptually different multidimensional vectorial data appearing in geo databases.

rasdaman is a domain-independent database management system (DBMS) which supports multidimensional arrays of any size and dimension and over freely definable cell types. Versatile interfaces allow rapid application deployment while a set of cutting-edge intelligent optimization techniques in the rasdaman server ensures fast, efficient access to large data sets, particularly in networked environments.

4.2.2. rasdaman Overall Architecture

The rasdaman client/server DBMS has been designed using internationally approved standards wherever possible. The system follows a two-tier client/server architecture with query processing completely done in the server. Internally and invisible to the application, arrays are decomposed into smaller units which are maintained in a conventional DBMS, for our purposes called the base DBMS.

On the other hand, the base DBMS usually will hold alphanumeric data (such as metadata) besides the array data. rasdaman offers means to establish references between arrays and alphanumeric data in both directions.

Hence, all multidimensional data go into the same physical database as the alphanumeric data, thereby considerably easing database maintenance (consistency, backup, etc.).

Figure 4.1 Embedding of rasdaman in IT infrastructure

Further information on application program interfacing, administration, and related topics is available in the other components of the rasdaman documentation set.

4.2.3. Interfaces

The syntactical elements explained in this document comprise the rasql language interface to rasdaman. There are several ways to actually enter such statements into the rasdaman system:

• By using the rasql command-line tool to send queries to rasdaman and get back the results.
• By developing an application program which uses the raslib/rasj function oql_execute() to forward query strings to the rasdaman server and get back the results.

RasLib are not the subject of this document. Please refer to the C++ Developer’s Guide or Java Developer’s Guide of the rasdaman documentation set for further information.

4.2.4. rasql and Standard SQL

The declarative interface to the rasdaman system consists of the rasdaman Query Language, rasql, which supports retrieval, manipulation, and data definition (replacing former rasdl).

Moreover, the rasdaman query language, rasql, is very similar - and in fact embeds into - standard SQL. Hence, if you are familiar with SQL, you will quickly be able to use rasql. Otherwise you may want to consult the introductory literature referenced at the end of this chapter.

The rasql language is, with only slight adaptations, being standardized by ISO as 9075 SQL Part 15: MDA (Multi-Dimensional Arrays).

4.2.5. Notational Conventions

The following notational conventions are used in this manual:

Program text (under this we also subsume queries in the document on hand) is printed in a monotype font. Such text is further differentiated into keywords and syntactic variables. Keywords like struct are printed in boldface; they have to be typed in as is.

An optional clause is enclosed in brackets; an arbitrary repetition is indicated through brackets and an ellipsis. Grammar alternatives can be grouped in parentheses separated by a | symbol.

Example

select resultList
from namedCollection [ [ as ] collIterator ]
     [ , namedCollection [ [ as ] collIterator ] ]...
[ where booleanExp ]

It is important not to mix the regular brackets [ and ] denoting array access, trimming, etc., with the grammar brackets [ and ] denoting optional clauses and repetition; in grammar excerpts the first case is in double quotes. The same applies to parentheses.

Italics are used in the text to draw attention to the first instance of a defined term in the text. In this case, the font is the same as in the running text, not Courier as in code pieces.

4.3. Terminology

4.3.1. An Intuitive Definition

An array is a set of elements which are ordered in space. The space considered here is discretized, i.e., only integer coordinates are admitted. The number of integers needed to identify a particular position in this space is called the dimension (sometimes also referred to as dimensionality). Each array element, which is referred to as cell, is positioned in space through its coordinates.

A cell can contain a single value (such as an intensity value in case of grayscale images) or a composite value (such as integer triples for the red, green, and blue component of a color image). All cells share the same structure which is referred to as the array cell type or array base type.

Implicitly a neighborhood is defined among cells through their coordinates: incrementing or decrementing any component of a coordinate will lead to another point in space. However, not all points of this (infinite) space will actually house a cell. For each dimension, there is a lower and upper bound, and only within these limits array cells are allowed; we call this area the spatial domain of an array. In the end, arrays look like multidimensional rectangles with limits parallel to the coordinate axes. The database developer defines both spatial domain and cell type in the array type definition. Not all bounds have to be fixed during type definition time, though: It is possible to leave bounds open so that the array can dynamically grow and shrink over its lifetime.

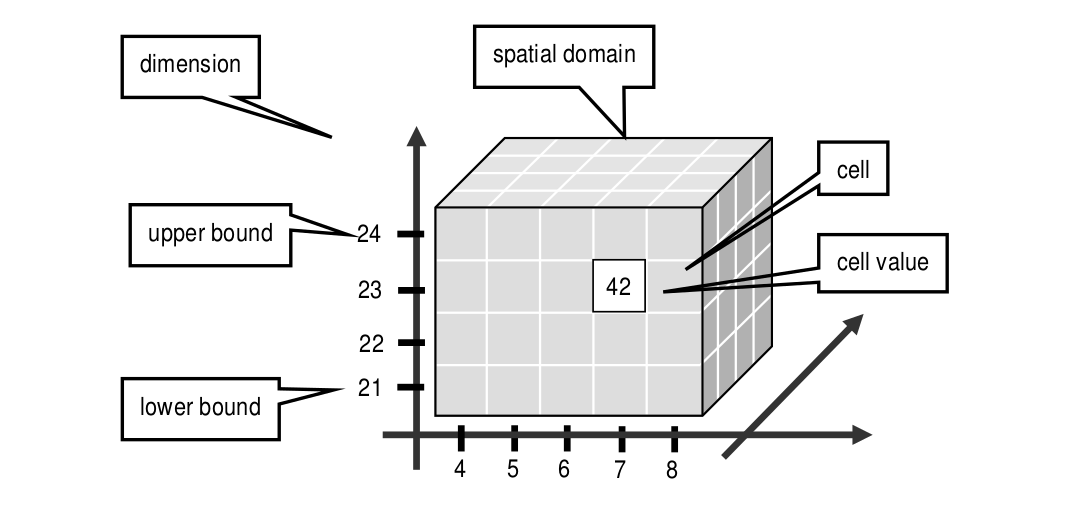
Figure 4.2 Constituents of an array

Synonyms for the term array are multidimensional arrays, multi­dimen­sional data, MDD. They are used interchangeably in the rasdaman documentation.

In rasdaman databases, arrays are grouped into collections. All elements of a collection share the same array type definition (for the remaining degrees of freedom see Array Type Definition). Collections form the basis for array handling, just as tables do in relational database technology.

4.3.2. A Technical Definition

Programmers who are familiar with the concept of arrays in programming languages maybe prefer this more technical definition:

An array is a mapping from integer coordinates, the spatial domain, to some data type, the cell type. An array’s spatial domain, which is always finite, is described by a pair of lower bounds and upper bounds for each dimension, resp. Arrays, therefore, always cover a finite, axis-parallel subset of Euclidean space.

Cell types can be any of the base types and composite types defined in the ODMG standard and known, for example from C/C++. In fact, every admissible C/C++ type is admissible in the rasdaman type system, too.

In rasdaman, arrays are strictly typed wrt. spatial domain and cell type. Type checking is done at query evaluation time. Type checking can be disabled selectively for an arbitrary number of lower and upper bounds of an array, thereby allowing for arrays whose spatial domains vary over the array lifetime.

4.4. Sample Database

4.4.1. Collection mr

This section introduces sample collections used later in this manual. The sample database which is shipped together with the system contains the schema and the instances outlined in the sequel.

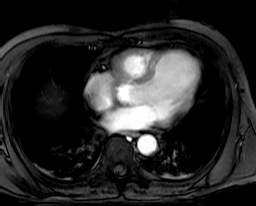
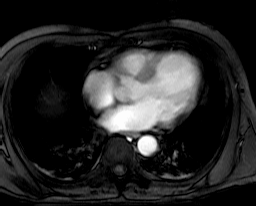
Collection mr consists of three images (see Figure 4.3) taken from the same patient using magnetic resonance tomography. Images are 8 bit grayscale with pixel values between 0 and 255 and a size of 256x211.

Figure 4.3 Sample collection mr

4.4.2. Collection mr2

Collection mr2 consists of only one image, namely the first image of collection mr (Figure 4.4). Hence, it is also 8 bit grayscale with size 256x211.

Figure 4.4 Sample collection mr2

4.4.3. Collection rgb

The last example collection, rgb, contains one item, a picture of the anthur flower (Figure 4.5). It is an RGB image of size 400x344 where each pixel is composed of three 8 bit integer components for the red, green, and blue component, resp.

Figure 4.5 The collection rgb

4.5. Type Definition Using rasdl

4.5.1. Overview

Every instance within a database is described by its data type (i.e., there is exactly one data type to which an instance belongs; conversely, one data type can serve to describe an arbitrary number of instances). Each database contains a self-contained set of such type definitions; no other type information, external to a database, is needed for database access.

A rasdaman schema contains three categories of data types:

• Cell type definitions; these can be base types (such as float) or composite (“struct”) types such as red/green/blue color pixels.
• MDD type definitions; these define arrays over some base type and with some spatial domain.
• Collection type definitions; they describe sets over some MDD type; collections of a given type can only contain MDD instances of the MDD type used in the definition.

Types are identified by their name which must be unique within a database; upper and lower case are distinguished. The same names are used in the C++ header files generated by the rasdl processor.

Type handling is done using the rasdl processor which allows adding types to a database schema, deleting types, displaying schema information, and generating C++ header files from database types. Therefore, rasdl is the tool for maintaining database schemata.

Dynamic Type Definition

New types can be defined dynamically while the rasdaman server is running. This means that new types introduced via rasdl are immediately available to all other applications after rasdl’s transaction commit.

Examples

In Examples examples are given for the most common rasdl tasks.

Important

Extreme care must be exercised on database and type maintenance. For example, deleting a database cannot be undone, and deleting a type still used in the database (i.e., which is needed to describe existing MDD objects) may make it impossible to access these database objects any more.

In general, database administration should be reserved to few persons, all of which should have high familiarity with the operating system, the relational database system, and the rasdaman system.

Alternative Type Definition

Creation of types is possible through rasql, too; see Type Definition Using rasql. For the future it is planned to phase out rasdl and perform all type management completely through rasql.

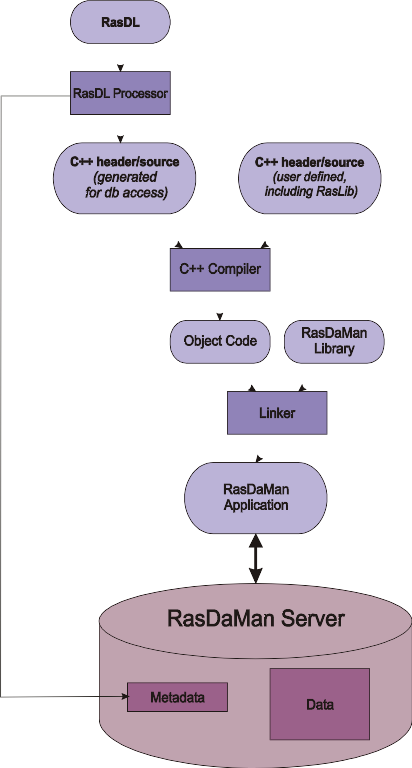
4.5.2. Application Development Workflow

The usual proceeding of setting up a database and an application operating this database consists of three major steps.

• First, a rasdl definition is established (best through a file, but also possible via typing in commands interactively) which is fed into the rasdl processor. The output generated from this source consists of C++ header and source files; in parallel, the type information is fed into the target database.
• In the second step, the program source code written by the application developer is compiled using the respective C++ compiler of the target platform. To this end, the header file generated in the first step as well as the RasLib header files are read by the compiler. The output is relocatable object code.
• In the third step, the so created rasdaman application executable can operate on a database with a structure as defined in the rasdl source used.

Figure 4.6 shows this application development workflow, including all the preprocess, compile and link steps necessary to generate an executable application.

Figure 4.6 Application development workflow

4.5.3. Type Definition

rasdl syntax closely follows C/C++ data type definition syntax [1]. In fact, there is only one syntactic extension to ODMG/C++ which allows to conveniently specify spatial domains. The complete syntax specification of rasdl can be found in the appendix.

Base Types

The set of standard data types, which is generated during creation of a database, materializes the base types defined in the ODMG standard (cf. Table 4.1).

Table 4.1 rasdaman base types

rasdl name	size	description
octet	8 bit	signed integer
char	8 bit	unsigned integer
short	16 bit	signed integer
unsigned short / ushort	16 bit	unsigned integer
long	32 bit	signed integer
unsigned long / ulong	32 bit	unsigned integer
float	32 bit	single precision floating point
double	64 bit	double precision floating point
complex	64 bit	single precision complex
complexd	128 bit	double precision complex
boolean	1 bit [2]	true (nonzero value), false (zero value)

Further cell types can be defined arbitrarily in rasdaman, based on the system-defined base types or other user-defined types. In particular, composite user-defined base types corresponding to struct s in C/C++ are supported. As a rule, every C/C++ type is admissible as array base type in rasdl with the exception of pointers (these are handled through OIDs, see Linking MDD with Other Data), nested arrays, and classes.

The keyword struct allows to define complex pixel types, typedef is used for the definition of MDD and set types in the same way as in C++. The typeName indicating the cell type of the array must be defined within the database schema using it.

Syntax

struct structName {
  attrType_1 attrName_1;
  ...
  attrType_n attrName_n;
};

Array Type Definition

A spatial domain can be defined with variable degree of freedom. The most concise way is to explicitly specify a lower and upper bound for each dimension. Such bounds are integer numbers whereby, in each dimension, the lower bound must be less or equal to the upper bound. Negative numbers are allowed, and the lower bound does not have to be 0.

Array ranges defined this way are checked by the server during every access. An attempt to access a cell outside the specified spatial domain will lead to a runtime error.

Syntax

typedef marray <typeName, [ lo_1 : hi_1, ..., lo_n : hi_n ]> marrayName;

Example

The following definition establishes a 5x5 integer array sitting in the center of the coordinate system. Such matrices can be used, for example, to hold convolution kernels.

typedef marray <int, [-2:2, -2:2]> kernel5;

Note that the symmetry in the boundaries grounds in the way kernels are defined; there is no constraint on the bounds in rasdl.

A higher degree of freedom in the array boundaries can be specified by indicating an asterisk “*” instead of a lower or upper bound at any position. In this case, range checking is disabled for that particular bound, and dynamic extending and shrinking is possible in that dimension.

Examples

A fax has a fixed width, but an arbitrary length. Modelling this requires to leave open the upper bound of the second dimension:

typedef marray <char, [ 1:1728, 1:* ]> G3Fax;

An array can have an arbitrary number of variable bounds:

typedef marray <char, [ *:*, *:* ]> GreyImage;

This extreme case - that all bounds are free - can be abbreviated by indicating, instead of the spatial domain in brackets, only the number of dimensions:

Syntax

typedef marray <typeName, dimension> marrayName;

Example

typedef marray <char, 2> GreyImage;

To leave open even the dimensionality of an array, even the dimension number can be omitted:

Syntax

typedef marray <typeName> marrayName;

Example

typedef set <GreyImage> GreySet;

It is recommended to use unbounded arrays with extreme care - all range checking is disabled, and structures may be created in the database which your (or your colleagues’) applications don’t expect.

Collection Type Definition

An array collection type is defined with the array type as parameter. A collection of such a type can contain an arbitrary number of arrays whereby each of these must conform with the array type indicated.

Syntax

typedef set <marrayName> setName;

Comments in Type Definitions

Comments are texts which are not evaluated by rasdaman in any way. However, they are useful - and should be used freely - for documentation purposes so that the defined type’s meaning will be clear to later readers.

Syntax

// any text, delimited by end of line

Example

struct RGBPixel // 3 x 8bit color pixels
{
  char red,     // red channel of color image
       green,   // green channel of color image
       blue;    // blue channel of color image
};

4.5.4. Sample Database Type Definitions

The following definitions describe the three sample collections introduced earlier.

Collections mr and mr2 share the same structure definition, namely 256x211 8-bit grayscale images. As we don’t want to restrict ourselves to a particular image size, we just define the image type as being 2-dimensional. The following fragment accomplishes this.

typedef marray <char, 2> GreyImage;
typedef set <GreyImage> GreySet;

Equivalently, but more verbosely, we could have specified the image type as

typedef marray <char,[ *:*, *:* ]> GreyImage;

The last example defines sets of RGB images. The first line defines the cell type as a struct containing three single-byte components. The next line defines an RGBImage as a 2-dimensional array of size 800x600 over base type RGBPixel. The last line defines a set of RGB images.

struct RGBPixel { char red, green, blue; };
typedef marray <RGBPixel, [0:799, 0:599]> RGBImage;
typedef set <RGBImage> RGBSet;

4.5.5. Deleting Types and Databases

For deleting a type or a whole database the rasdl --delX command family is provided where X is one of database, basetype, mddtype, or settype:

--deldatabase db
	delete database db [3]
--delbasetype type
	delete base type type from database
--delmddtype type
	delete MDD type type from database
--delsettype type
	delete set (collection) type type

Important

Extreme care must be exercised on database and type maintenance. Deleting a database cannot be undone, and deleting a type still used in the database (i.e., which is needed to describe existing MDD objects) may make it impossible to access these database objects any more.

In general, database administration should be reserved to few persons, all of which should have high familiarity with the operating system, the relational database system, and the rasdaman system.

Example

The following Unix command line will delete the definition of set type MyCollectionType from database RASBASE; it is the responsibility of the rasdl user (i.e., the database administrator) to ensure that no instances of this set definition exist in the database.

rasdl --database RASBASE --delsettype MyCollectionType

4.5.6. rasdl Invocation

As outlined, the rasdl processor reads the specified rasdl source file, imports the schema information into the database, and generates a corresponding C++ header file. A rasdl source file has to be self-contained, i.e., only types which are defined in the same file are allowed to be used for definitions. Types must be defined before use.

Usage:

rasdl [options]

Options:

--database db	name of database (default: RASBASE)
--connect connectstr
	connect string for base DBMS connection (e.g. test/test@julep) default: / Note: the connect parameter is ignored is when rasdaman configure for using file-based storage
-c, --createdatabase dbname
	create database with name dbname and initialize it with the standard schema
--deldatabase db
	delete database db
--delbasetype type
	delete base type type from database
--delmddtype type
	delete MDD type type from database
--delsettype type
	delete set (collection) type type from database
-h, --help	help: display invocation syntax
-p, --print db	print all data type definitions in database db
-r, --read file
	read rasdl commands from file file
-i, --insert	insert types into database (-r required)
--hh file	generate C++ header file file (-r required)

Note

Right now, rasdl is a server-based utility, which means it must be invoced on the machine where the rasdaman server runs.

Note

The -c option for database creation is dependent on the base DBMS used – some systems do, a very few don’t allow database creation through rasdl.

4.5.7. Examples

Default database name is RASBASE. It depends upon the base DBMS whether upper and lower case are distinguished (usually they are not).

Create Database

A new database is created through

rasdl -c

An error message is issued and the operation is aborted if the database exists already.

Delete Database

An existing database is deleted through

rasdl --deldatabase

All contents will be lost irretrievably. All space in the base DBMS is released, all tables (including rasdaman system tables) are removed.

Read Type Definition File

A type definition file named myfile is read into the database through

rasdl -r myfile -i

In particular, the standard types must be read in as part of the database creation process:

rasdl -r ~rasdaman/examples/rasdl/basictypes.dl -i

Print All Types

An overview on all rasdaman types defined is printed through

rasdl -p

4.6. Type Definition Using rasql

Starting with rasdaman version 9, DDL commands have been added to rasql which can take over most of the tasks rasdl (see Type Definition Using rasdl) accomplishes.

Types in rasdaman establish a 3-level hierarchy:

• Struct types allow defining composite cell types, in addition to the predefined atomic cell types.
• Array types allow defining array structures, given by a cell type (using an atomic or struct type) and a domain extent.
• Set types allow defining collections (sets) over arrays of some particular array type.

Both variants can be used in parallel (and manipulate the same data dictionary in the server). In future, it is planned to phase out rasdl completely as it has been crafted along the (meantime obsolete) ODMG standard whereas rasdaman is aiming at a tight integration with SQL, in particular at implementing the forthcoming SQL/MDA standard.

4.6.1. Cell types

Base types

The base types supported are listed in Table 4.1.

Composite types

Definition of composite types adheres to the following syntax:

create type typeName
as (
  attrName_1 attrType_1 ,
  attrName_1 attrType_1 ,
  ...
  attrName_n attrType_n
)

Attribute names must be unique within a composite type, otherwise an exception is thrown.

Example

An RGB pixel type can be defined as

create type RGBPixel
as (
  red char,
  green char,
  blue char
)

4.6.2. Array types

An marray (“multi-dimensional array”) type defines an array type through its cell type (see Cell types) and its dimensionality.

Array type syntax

The syntax for creating an marray type is as below. There are two variants, corresponding to the dimensionality specification alternatives described above:

create type typeName
as baseTypeName mdarray domainSpec

where baseTypeName is the name of a defined cell type and domainSpec is a multi-dimensional interval specification as described below.

Alternatively, a cell type structure can be indicated directly:

create type typeName as
(
  attrName_1 attrType_1,
  ...,
  attrName_n attrType_n
) mdarray domainSpec

No type (of any kind) with name typeName may pre-exist already, otherwise an exception is thrown.

Attribute names must be unique within a composite type, otherwise an exception is thrown.

Array dimensionality

Dimensions and their extents are specified by providing an axis name for each dimension and, optionally, a lower and upper bound:

[ a_1 ( lo_1 : hi_1 ), ... , a_d ( lo_d : hi_d ) ]
[ a_1 , ... , a_d ]

where d is a positive integer number, a_i are identifiers, and lo_1 and hi_1 are integers with lo_1 le hi_1. Both lo_1 and hi_1 can be an asterisk (*) instead of a number, in which case there is no limit in the particular direction of the axis. If the bounds lo_1 and hi_1 on a particular axis are not specified, they are assumed to be equivalent to *.

Axis names must be unique within a domain specification, otherwise an exception is thrown.

Currently (rasdaman 9) axis names are ignored and cannot be used in queries yet.

Examples

The following statement defines a 2-D XGA RGB image, based on the definition of RGBPixel as shown above:

create type RGBImage
as RGBPixel mdarray [ x ( 0:1023 ), y ( 0:767 ) ]

An 2-D image without any extent limitation can be defined through:

create type UnboundedImage
as RGBPixel mdarray [ x, y ]

Selectively we can also limit only the bounds on the x axis for example:

create type PartiallyBoundedImage
as RGBPixel mdarray [ x ( 0 : 1023 ), y ]

Note

The reader may notice that the syntax in rasql is changed over the original rasdl syntax. For example, the keyword marray is changed to mdarray in the rasql type definition. This has been done in pre­paration of the rasql syntax for the forthcoming ISO SQL/MDA (“Multidimensional Arrays”) standard.

4.6.3. Set types

A set type defines a collection of arrays sharing the same marray type. Additionally, a collection can also have null values which are used in order to characterise sparse arrays. A sparse array is an array where most of the elements have a null value.

Set type syntax

create type typeName
as set ( marrayTypeName [ nullValues ] )

where marrayTypeName is the name of a defined marray type and null­Values is an optional specification of a set of values to be treated as nulls (cf. Null Values).

No object with name typeName may pre-exist already.

Null Values

The optional nullValues clause in a set type definition (which is identical to the specification given in Null Values) adheres to the following syntax:

null values [ ( double | [ double : double ] )
          ( , ( double | [ double : double ] ) )* ]

Example

For example, the following statement defines a set type of 2-D XGA RGB images, based on the definition of RGBImage:

create type RGBSet
as set ( RGBImage )

If values 0, 253, 254, and 255 are to be considered null values, this can be specified as follows:

create type RGBSet
as set ( RGBImage null values [ 0, 253 : 255 ] )

Note that these null values will apply equally to every band. It is not possible to separate null values per band.

4.6.4. Drop type

A type definition can be dropped (i.e., deleted from the database) if it is not in use. This is the case if both of the following conditions hold:

• The type is not used in any other type definition.
• There are no array instances existing which are based, directly or indirectly, on the type on hand.

Further, base types (such as char) cannot be deleted.

Drop type syntax

drop type typeName

4.6.5. List available types

A list of all types defined in the database can be obtained in textual form, adhering to the rasql type definition syntax. This is done by querying virtual collections (similar to the virtual collection RAS_COLLECT­ION_­NAMES).

Technically, the output of such a query is a list of 1-D char arrays, each one containing one type definition.

List type syntax

select typeColl from typeColl

where typeColl is one of

• RAS_STRUCT_TYPES for struct types
• RAS_MARRAY_TYPES for array types
• RAS_SET_TYPES for set types

Usage notes

Collection aliases can be used, such as:

select t from RAS_STRUCT_TYPES as t

No operations can be performed on the output array.

Example output

A struct types result may look like this when printed:

create type RGBPixel
as ( red char, green char, blue char )

create type TestPixel
as ( band1 char, band2 char, band3 char )

create type GeostatPredictionPixel
as ( prediction float, variance float )

An marray types result may look like this when printed:

create type GreyImage
as char mdarray [ x, y ]

create type RGBCube
as RGBPixel mdarray [ x, y, z ]

create type XGAImage
as RGBPixel mdarray [ x ( 0 : 1023 ), y ( 0 : 767 ) ]

A set types result may look like this when printed:

create type GreySet
as set ( GreyImage )

create type NullValueTestSet
as set ( NullValueArrayTest null values [5:7] )

4.6.6. Changing types

The type of an existing collection can be changed to another type through the alter statement.

The new collection type must be compatible with the old one, which means:

• same cell type
• same dimensionality
• no domain shrinking

Changes are allowed, for example, in the null values.

Alter type syntax

alter collection collName set type collType

where

• collName is the name of an existing collection
• collType is the name of an existing collection type

Usage notes

The collection does not need to be empty, i.e. it may contain array objects.

Currently, only set (i.e., collection) types can be modified.

Example

A struct types result may look like this when printed:

alter collection Bathymetry
set type BathymetryWithNullValues

4.7. Query Execution with rasql

The rasdaman toolkit offers essentially three ways to communicate with a database through queries:

• By writing a C++ or Java application that uses the rasdaman APIs, raslib or rasj, resp. (see the rasdaman API guides).
• By writing queries using the GUI-based rview tool which allows to visualize results in a large variety of display modes (see the rasdaman rview Guide).
• By submitting queries via command line using rasql; this tool is covered in this section.

The rasql tool accepts a query string (which can be parametrised as explained in the API guides), sends it to the server for evaluation, and receives the result set. Results can be displayed in alphanumeric mode, or they can be stored in files.

4.7.1. Examples

For the user who is familiar with command line tools in general and the rasql query language, we give a brief introduction by way of examples. They outline the basic principles through common tasks.

• Create a collection test of type GreySet (note the explicit setting of user rasadmin; rasql’s default user rasguest by default cannot write):

  rasql -q "create collection test GreySet" \
        --user rasadmin --passwd rasadmin
  

• Print the names of all existing collections:

  rasql -q "select r from RAS_COLLECTIONNAMES as r" \
        --out string
  

• Export demo collection mr into TIFF files rasql_1.tif, rasql_2.tif, rasql_3.tif (note the escaped double-quotes as required by shell):

  rasql -q "select encode(m, \"tiff\") from mr as m"
        --out file
  

• Import TIFF file myfile into collection mr as new image (note the different query string delimiters to preserve the $ character!):

  rasql -q 'insert into mr values decode($1)' \
        -f myfile --user rasadmin --passwd rasadmin
  

• Put a grey square into every mr image:

  rasql -q "update mr as m set m[0:10,0:10] \
            assign marray x in [0:10,0:10] values 127c" \
        --user rasadmin --passwd rasadmin
  

• Verify result of update query by displaying pixel values as hex numbers:

  rasql -q "select m[0:10,0:10] from mr as m" --out hex
  

4.7.2. Invocation syntax

Rasql is invoked as a command with the query string as parameter. Additional parameters guide detailed behavior, such as authentication and result display.

Any errors or other diagnostic output encountered are printed; transactions are aborted upon errors.

Usage:

rasql [--query q|-q q] [options]

Options:

-h, --help	show command line switches
-q, --query q	query string to be sent to the rasdaman server for execution
-f, --file f	file name for upload through $i parameters within queries; each $i needs its own file parameter, in proper sequence [4]. Requires –mdddomain and –mddtype
--content	display result, if any (see also –out and –type for output formatting)
--out t	use display method t for cell values of result MDDs where t is one of none: do not display result item contents file: write each result MDD into a separate file string: print result MDD contents as char string (only for 1D arrays of type char) hex: print result MDD cells as a sequence of space-separated hex values formatted: reserved, not yet supported Option –out implies –content; default: none
--outfile of	file name template for storing result images (ignored for scalar results). Use ‘%d’ to indicate auto numbering position, like with printf(1). For well-known file types, a proper suffix is appended to the resulting file name. Implies –out file. (default: rasql_%d)
--mdddomain d	MDD domain, format: ‘[x0:x1,y0:y1]’; required only if –file specified and file is in data format r_Array; if input file format is some standard data exchange format and the query uses a convertor, such as encode($1,”tiff”), then domain information can be obtained from the file header.
--mddtype t	input MDD type (must be a type defined in the database); required only if –file specified and file is in data format r_Array; if input file format is some standard data exchange format and the query uses a convertor, such as decode($1,”tiff”), then type information can be obtained from the file header.
--type	display type information for results
-s, --server h	rasdaman server name or address (default: localhost)
-p, --port p	rasdaman port number (default: 7001)
-d, --database db
	name of database (default: RASBASE)
--user u	name of user (default: rasguest)
--passwd p	password of user (default: rasguest)

4.8. Overview: General Query Format

4.8.1. Basic Query Mechanism

rasql provides declarative query functionality on collections (i.e., sets) of MDD stored in a rasdaman database. The query language is based on the SQL-92 standard and extends the language with high-level multidimensional operators.

The general query structure is best explained by means of an example. Consider the following query:

select mr[100:150,40:80] / 2
from mr
where some_cells( mr[120:160, 55:75] > 250 )

In the from clause, mr is specified as the working collection on which all evaluation will take place. This name, which serves as an “iterator variable” over this collection, can be used in other parts of the query for referencing the particular collection element under inspection.

Optionally, an alias name can be given to the collection (see syntax below) - however, in most cases this is not necessary.

In the where clause, a condition is phrased. Each collection element in turn is probed, and upon fulfillment of the condition the item is added to the query result set. In the example query, part of the image is tested against a threshold value.

Elements in the query result set, finally, can be “post-processed” in the select clause by applying further operations. In the case on hand, a spatial extraction is done combined with an intensity reduction on the extracted image part.

In summary, a rasql query returns a set fulfilling some search condition just as is the case with conventional SQL and OQL. The difference lies in the operations which are available in the select and where clause: SQL does not support expressions containing multi­dimen­sional operators, whereas rasql does.

Syntax

select resultList
from collName [ as collIterator ]
[ , collName [ as collIterator ] ] ...
[ where booleanExp ]

The complete rasql query syntax can be found in the Appendix.

4.8.2. Select Clause: Result Preparation

Type and format of the query result are specified in the select part of the query. The query result type can be multidimensional, a struct, or atomic (i.e., scalar). The select clause can reference the collection iteration variable defined in the from clause; each array in the collection will be assigned to this iteration variable successively.

Example

Images from collection mr, with pixel intensity reduced by a factor 2:

select mr / 2
from mr

4.8.3. From Clause: Collection Specification

In the from clause, the list of collections to be inspected is specified, optionally together with a variable name which is associated to each collection. For query evaluation the cross product between all participating collections is built which means that every possible combination of elements from all collections is evaluated. For instance in case of two collections, each MDD of the first collection is combined with each MDD of the second collection. Hence, combining a collection with n elements with a collection containing m elements results in n*m combinations. This is important for estimating query response time.

Example

The following example subtracts each MDD of collection mr2 from each MDD of collection mr (the binary induced operation used in this example is explained in Binary Induction).

select mr - mr2
from mr, mr2

Using alias variables a and b bound to collections mr and mr2, resp., the same query looks as follows:

select a - b
from mr as a, mr2 as b

Cross products

As in SQL, multiple collections in a from clause such as

from c1, c2, ..., ck

are evaluated to a cross product. This means that the select clause is evaluated for a virtual collection that has n1 * n2 * … * nk elements if c1 contains n1 elements, c2 contains n2 elements, and so forth.

Warning: This holds regardless of the select expression - even if you mention only say c1 in the select clause, the number of result elements will be the product of all collection sizes!

4.8.4. Where Clause: Conditions

In the where clause, conditions are specified which members of the query result set must fulfil. Like in SQL, predicates are built as boolean expressions using comparison, parenthesis, functions, etc. Unlike SQL, however, rasql offers mechanisms to express selection criteria on multidimensional items.

Example

We want to restrict the previous result to those images where at least one difference pixel value is greater than 50 (see Binary Induction):

select mr - mr2
from mr, mr2
where some_cells( mr - mr2 > 50 )

4.8.5. Comments in Queries

Comments are texts which are not evaluated by the rasdaman server in any way. However, they are useful - and should be used freely - for documentation purposes; in particular for stored queries it is important that its meaning will be clear to later readers.

Syntax

-- any text, delimited by end of line

Example

select mr -- this comment text is ignored by rasdaman
from mr   -- for comments spanning several lines,
          -- every line needs a separate '--' starter

4.9. Constants

4.9.1. Atomic Constants

Atomic constants are written in standard C/C++ style. If necessary con­stants are augmented with a one or two letter postfix to un­ambiguously determine its data type (Table 4.2).

The default for integer constants is ‘L’, for floats it is ‘F’. Specifiers are case insensitive.

Example

25c
-1700L
.4e-5D

Note

Boolean constants true and false are unique, so they do not need a length specifier.

Table 4.2 Data type specifiers

postfix	type
c	char
o	octet
s	short
us	unsigned short
l	long
ul	unsigned long
f	float
d	double

Additionally, the following special floating-point constants are supported as well:

Table 4.3 Special floating-point constants corresponding to IEEE 754 NaN and Inf.

Constant	Type
NaN	double
NaNf	float
Inf	double
Inff	float

4.9.2. Composite Constants

Composite constants resemble records (“structs”) over atomic con­stants or other records. Notation is as follows.

Syntax

struct { const_0, ..., const_n }

where const_i can be atomic or a struct again.

Example

struct{ struct{ 1l, 2l, 3l }, true }

Complex numbers

Special built-in structs are complex and complexd for single and double precision complex numbers, resp. The constructor is defined by

Syntax

complex( re, im )

where re and im are floating point expressions. The resulting complex constant is of type complexd if at least one of the constituent expressions is double precision, otherwise the result is of type complex.

Example

complex( .35, 16.0d )

Component access

See Struct Component Selection for details on how to extract the constituents from a composite value.

4.9.3. Array Constants

Small array constants can be indicated literally. An array constant consists of the spatial domain specification (see Spatial Domain) followed by the cell values whereby value sequencing is as follow. The array is linearized in a way that the lowest dimension [5] is the “outermost” dimension and the highest dimension [6] is the “innermost” one. Within each dimension, elements are listed sequentially, starting with the lower bound and proceeding until the upper bound. List elements for the innermost dimension are separated by comma “,”, all others by semicolon “;”.

The exact number of values as specified in the leading spatial domain expression must be provided. All constants must have the same type; this will be the result array’s base type.

Syntax

< mintervalExp
  scalarList_0 ; ... ; scalarList_n ; >

where scalarList is defined as a comma separated list of literals:

scalar_0, scalar_1, ... scalar_n ;

Example

< [-1:1,-2:2] 0, 1, 2, 3, 4;
              1, 2, 3, 4, 5;
              2, 3, 4, 5, 6 >

This constant expression defines the following matrix:

4.9.4. Object identifier (OID) Constants

OIDs serve to uniquely identify arrays (see Linking MDD with Other Data). Within a database, the OID of an array is an integer number. To use an OID outside the context of a particular database, it must be fully qualified with the system name where the database resides, the name of the database containing the array, and the local array OID.

The worldwide unique array identifiers, i.e., OIDs, consist of three components:

• A string containing the system where the database resides (system name),
• A string containing the database (“base name”), and
• A number containing the local object id within the database.

The full OID is enclosed in ‘<’ and ‘>’ characters, the three name com­ponents are separated by a vertical bar ‘|’.

System and database names obey the naming rules of the underlying operating system and base DBMS, i.e., usually they are made up of lower and upper case characters, underscores, and digits, with digits not as first character. Any additional white space (space, tab, or newline characters) inbetween is assumed to be part of the name, so this should be avoided.

The local OID is an integer number.

Syntax

< systemName | baseName | objectID >
objectID

where systemName and baseName are string literals and objectID is an integerExp.

Example

< acme.com | RASBASE | 42 >
42

4.9.5. String constants

A sequence of characters delimited by double quotes is a string.

Syntax

"..."

Example

SELECT encode(coll, "png") FROM coll

4.9.6. Collection Names

Collections are named containers for sets of MDD objects (see Linking MDD with Other Data). A collection name is made up of lower and upper case characters, underscores, and digits. Depending on the underlying base DBMS, names may be limited in length, and some systems (rare though) may not distinguish upper and lower case letters. Please refer to the rasdaman External Products Integration Guide for details on your par­ticular platform.

Operations available on name constants are string equality “=” and inequality “!=”.

4.10. Spatial Domain Operations

4.10.1. One-Dimensional Intervals

One-dimensional (1D) intervals describe non-empty, consecutive sets of integer numbers, described by integer-valued lower and upper bound, resp.; negative values are admissible for both bounds. Intervals are specified by indicating lower and upper bound through integer-valued expressions according to the following syntax:

The lower and upper bounds of an interval can be extracted using the functions .lo and .hi.

Syntax

integerExp_1 : integerExp_2
intervalExp.lo
intervalExp.hi

A one-dimensional interval with integerExp_1 as lower bound and integerExp_2 as upper bound is constructed. The lower bound must be less or equal to the upper bound. Lower and upper bound extrac­tors return the integer-valued bounds.

Examples

An interval ranging from -17 up to 245 is written as:

-17 : 245

Conversely, the following expression evaluates to 245; note the parenthesis to enforce the desired evaluation sequence:

(-17 : 245).hi

4.10.2. Multidimensional Intervals

Multidimensional intervals (m-intervals) describe areas in space, or better said: point sets. These point sets form rectangular and axis-parallel “cubes” of some dimension. An m-interval’s dimension is given by the number of 1D intervals it needs to be described; the bounds of the “cube” are indicated by the lower and upper bound of the respective 1D interval in each dimension.

From an m-interval, the intervals describing a particular dimension can be extracted by indexing the m-interval with the number of the desired dimension using the operator [].

Dimension counting in an m-interval expression runs from left to right, starting with lowest dimension number 0.

Syntax

[ intervalExp_0 , ... , intervalExp_n ]
[ intervalExp_0 , ... , intervalExp_n ] [integerExp ]

An (n+1)-dimensional m-interval with the specified intervalExp_i is built where the first dimension is described by intervalExp_0, etc., until the last dimension described by intervalExp_n.

Example

A 2-dimensional m-interval ranging from -17 to 245 in dimension 1 and from 42 to 227 in dimension 2 can be denoted as

[ -17 : 245, 42 : 227 ]

The expression below evaluates to [42:227].

[ -17 : 245, 42 : 227 ] [1]

…whereas here the result is 42:

[ -17 : 245, 42 : 227 ] [1].lo

4.11. Array Operations

As we have seen in the last Section, intervals and m-intervals describe n-dimensional regions in space.

Next, we are going to place information into the regular grid estab­lished by the m-intervals so that, at the position of every integer-valued coordinate, a value can be stored. Each such value container addressed by an n-dimensional coordinate will be referred to as a cell. The set of all the cells described by a particular m-interval and with cells over a particular base type, then, forms the array.

As before with intervals, we introduce means to describe arrays through expressions, i.e., to derive new arrays from existing ones. Such operations can change an arrays shape and dimension (some­times called geometric operations), or the cell values (referred to as value-changing operations), or both. In extreme cases, both array dimension, size, and base type can change completely, for example in the case of a histogram computation.

First, we describe the means to query and manipulate an array’s spatial domain (so-called geometric operations), then we introduce the means to query and manipulate an array’s cell values (value-changing operations).

Note that some operations are restricted in the operand domains they accept, as is common in arithmetics in programming languages; division by zero is a common example. Arithmetic Errors and Other Exception Situations contains information about possible error conditions, how to deal with them, and how to prevent them.

4.11.1. Spatial Domain

The m-interval covered by an array is called the array’s spatial domain. Function sdom() allows to retrieve an array’s current spatial domain. The current domain of an array is the minimal axis-parallel bounding box containing all currently defined cells.

As arrays can have variable bounds according to their type definition (see Array Type Definition), their spatial domain cannot always be determined from the schema information, but must be recorded individually by the database system. In case of a fixed-size array, this will coincide with the schema information, in case of a variable-size array it delivers the spatial domain to which the array has been set. The operators presented below and in Update allow to change an array’s spatial domain. Notably, a collection defined over variable-size arrays can hold arrays which, at a given moment in time, may differ in the lower and/or upper bounds of their variable dimensions.

Syntax

sdom( mddExp )

Function sdom() evaluates to the current spatial domain of mddExp.

Examples

Consider an image a of collection mr. Elements from this collection are defined as having free bounds, but in practice our collection elements all have spatial domain [0 : 255, 0 : 210]. Then, the following equi­valences hold:

sdom(a)       = [0 : 255, 0 : 210]
sdom(a)[0]    = [0 : 255]
sdom(a)[0].lo = 0
sdom(a)[0].hi = 255

4.11.2. Geometric Operations

Trimming

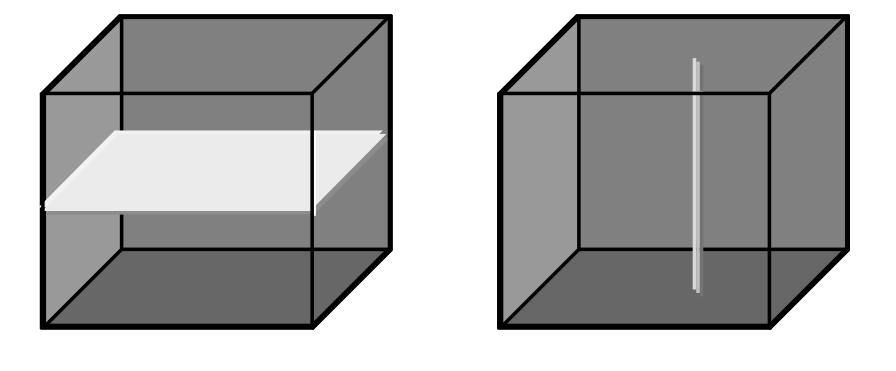
Reducing the spatial domain of an array while leaving the cell values unchanged is called trimming. Array dimension remains unchanged.

Figure 4.7 Spatial domain modification through trimming (2-D example)

The generalized trim operator allows restriction, extension, and a combination of both operations in a shorthand syntax. This operator does not check for proper subsetting or supersetting of the domain modifier.

Syntax

mddExp [ mintervalExp ]

Examples

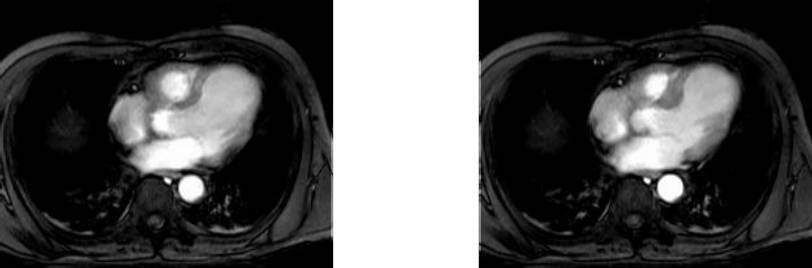
The following query returns cutouts from the area [120: 160 , 55 : 75] of all images in collection mr (see Figure 4.8).

select mr[ 120:160, 55:75 ]
from mr

Figure 4.8 Trimming result

Section

A section allows to extract lower-dimen­sional layers (“slices”) from an array.

Figure 4.9 Single and double section through 3-D array, yielding 2-D and 1-D sections.

A section is accomplished through a trim expression by indicating the slicing position rather than a selection interval. A section can be made in any dimension within a trim expression. Each section reduces the dimension by one.

Syntax

mddExp [ integerExp_0 , ... , integerExp_n ]

This makes sections through mddExp at positions integerExp_i for each dimension i.

Example

The following query produces a 2-D section in the 2^nd dimension of a 3-D cube:

select Images3D[ 0:256, 10, 0:256 ]
from Images3D

Note

If a section is done in every dimension of an array, the result is one single cell. This special case resembles array element access in programming languages, e.g., C/C++. However, in rasql the result still is an array, namely one with zero dimensions and exactly one element.

Example

The following query delivers a set of 0-D arrays containing single pixels, namely the ones with coordinate [100,150]:

select mr[ 100, 150 ]
from mr

The Array Bound Wildcard Operator “*”

An asterisk “*” can be used as a shorthand for an sdom() invocation in a trim expression; the following phrases all are equivalent:

a [ *:*, *:* ] = a [ sdom(a)[0] , sdom(a)[1] ]
               = a [ sdom(a)[0].lo : sdom(a)[0].hi ,
                     sdom(a)[1].lo : sdom(a)[1].hi ]

An asterisk “*” can appear at any lower or upper bound position within a trim expression denoting the current spatial domain boundary. A trim expression can contain an arbitrary number of such wildcards. Note, however, that an asterisk cannot be used for specifying a section.

Example

The following are valid applications of the asterisk operator:

select mr[ 50:*, *:200 ]
from mr

select mr[ *:*, 10:150 ]
from mr

The next is illegal because it attempts to use an asterisk in a section:

select mr[ *, 100:200 ] -- illegal "*" usage in dimension 0
from mr

Note

It is well possible (and often recommended) to use an array’s spatial domain or part of it for query formulation; this makes the query more general and, hence, allows to establish query libraries. The following query cuts away the rightmost pixel line from the images:

select mr[ *:*, *:sdom(mr)[1].hi - 1 ]   -- good, portable
from mr

In the next example, conversely, trim bounds are written explicitly; this query’s trim expression, therefore, cannot be used with any other array type.

select mr[ 0:767, 0:1023 ]               -- bad, not portable
from mr

One might get the idea that the last query evaluates faster. This, however, is not the case; the server’s intelligent query engine makes the first version execute at just the same speed.

Shifting a Spatial Domain

Built-in function shift() transposes an array: its spatial domain remains unchanged in shape, but all cell contents simultaneously are moved to another location in n-dimensional space. Cell values themselves remain un­changed.

Syntax

shift( mddExp , pointExp )

The function accepts an mddExp and a pointExp and returns an array whose spatial domain is shifted by vector pointExp.

Example

The following expression evaluates to an array with spatial domain [3:13, 4:24]. Containing the same values as the original array a.

shift( a[ 0:10, 0:20 ], [ 3, 4 ] )

Extending a Spatial Domain

Function extend() enlarges a given MDD with the domain specified. The domain for extending must, for every boundary element, be at least as large as the MDD’s domain boundary. The new MDD contains 0 values in the extended part of its domain and the MDD’s original cell values within the MDD’s domain.

Syntax

extend( mddExp , mintervalExp )

The function accepts an mddExp and a mintervalExp and returns an array whose spatial domain is extended to the new domain specified by mintervalExp. The result MDD has the same cell type as the input MDD.

Precondition:

sdom( mddExp ) contained in mintervalExp

Example

Assuming that MDD a has a spatial domain of [0:50, 0:25], the following expression evaluates to an array with spatial domain [-100:100, -50:50], a’s values in the subdomain [0:50, 0:25], and 0 values at the remaining cell positions.

extend( a, [-100:100, -50:50] )

Geographic projection

Overview

“A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties.” (Wikipedia)

Each coordinate tieing a geographic object, map, or pixel to some position on earth (or some other celestial object, for that matter) is valid only in conjunction with the Coordinate Reference System (CRS) in which it is expressed. For 2-D Earth CRSs, a set of CRSs and their identifiers is normatively defined by the OGP Geomatics Committee, formed in 2005 by the absorption into OGP of the now-defunct European Petroleum Survey Group (EPSG). By way of tradition, however, this set of CRS definitions still is known as “EPSG”, and the CRS identifiers as “EPSG codes”. For example, EPSG:4326 references the well-known WGS84 CRS.

The project() function

Assume an MDD object M and two CRS identifiers C1 and C2 such as “EPSG:4326”. The project() function establishes an output MDD, with same dimension as M, whose contents is given by projecting M from CRS C1 into CRS C2.

The project() function comes in several variants based on the provided input arguments

(1) project( mddExpr, boundsIn, crsIn, crsOut )

(2) project( mddExpr, boundsIn, crsIn, boundsOut, crsOut,
                      widthOut, heightOut )

(3) project( mddExpr, boundsIn, crsIn, boundsOut, crsOut,
                      widthOut, heightOut, resampleAlg, errThreshold )

where

• mddExpr - MDD object to be reprojected.

• boundsIn - geographic bounding box given as a string of comma-separated floating-point values of the format: "xmin, ymin, xmax, ymax".

• crsIn - geographic CRS as a string. Internally, the project() function is mapped to GDAL; hence, it accepts the same CRS formats as GDAL:

  • Well Known Text (as per GDAL)
  • “EPSG:n”
  • “EPSGA:n”
  • “AUTO:proj_id,unit_id,lon0,lat0” indicating OGC WMS auto projections
  • “urn:ogc:def:crs:EPSG::n” indicating OGC URNs (deprecated by OGC)
  • PROJ.4 definitions
  • well known names, such as NAD27, NAD83, WGS84 or WGS72.
  • WKT in ESRI format, prefixed with “ESRI::”
  • “IGNF:xxx” and “+init=IGNF:xxx”, etc.
  • Since recently (v1.10), GDAL also supports OGC CRS URLs, OGC’s preferred way of identifying CRSs.

• boundsOut - geographic bounding box of the projected output, given in the same format as boundsIn. This can be “smaller” than the input bounding box, in which case the input will be cropped.

• crsOut - geographic CRS of the result, in same format as crsIn.

• widthOut, heightOut - integer grid extents of the result; the result will be accordingly scaled to fit in these extents.

• resampleAlg - resampling algorithm to use, equivalent to the ones in GDAL:

  near

  Nearest neighbour (default, fastest algorithm, worst interpolation quality).

  bilinear

  Bilinear resampling (2x2 kernel).

  cubic

  Cubic convolution approximation (4x4 kernel).

  cubicspline

  Cubic B-spline approximation (4x4 kernel).

  lanczos

  Lanczos windowed sinc (6x6 kernel).

  average

  Average of all non-NODATA contributing pixels. (GDAL >= 1.10.0)

  mode

  Selects the value which appears most often of all the sampled points. (GDAL >= 1.10.0)

  max

  Selects the maximum value from all non-NODATA contributing pixels. (GDAL >= 2.0.0)

  min

  Selects the minimum value from all non-NODATA contributing pixels. (GDAL >= 2.0.0)

  med

  Selects the median value of all non-NODATA contributing pixels. (GDAL >= 2.0.0)

  q1

  Selects the first quartile value of all non-NODATA contributing pixels. (GDAL >= 2.0.0)

  q3

  Selects the third quartile value of all non-NODATA contributing pixels. (GDAL >= 2.0.0)

• errThreshold - error threshold for transformation approximation (in pixel units - defaults to 0.125).

Example

The following expression projects the MDD worldMap with bounding box “-180, -90, 180, 90” in CRS EPSG 4326, into EPSG 54030:

project( worldMap, "-180, -90, 180, 90", "EPSG:4326", "EPSG:54030" )

The next example reprojects a subset of MDD Formosat with geographic bbox “265725, 2544015, 341595, 2617695” in EPSG 32651, to bbox “120.630936455 23.5842129067 120.77553782 23.721772322” in EPSG 4326 fit into a 256 x 256 pixels area. The resampling algorithm is set to bicubic, and the pixel error threshold is 0.1.

project( Formosat[ 0:2528, 0:2456 ],
  "265725, 2544015, 341595, 2617695", "EPSG:32651",
  "120.630936455 23.5842129067 120.77553782 23.721772322", "EPSG:4326",
  256, 256, bicubic, 0.1 )

Limitations

Only 2-D arrays are supported. For multiband arrays, all bands must be of the same cell type.

Notes

Reprojection implies resampling of the cell values into a new grid, hence usually they will change.

As for the resampling process typically a larger area is required than the reprojected data area itself, it is advisable to project an area smaller than the total domain of the MDD.

Per se, rasdaman is a domain-agnostic Array DBMS and, hence, does not know about CRSs; specific geo semantics is added by rasdaman’s petascope layer. However, for the sake of performance, the reprojection capability – which in geo service practice is immensely important – is pushed down into rasdaman, rather than doing reprojection in petascope’s Java code. To this end, the project() function provides rasdaman with enough information to perform a reprojection, however, without “knowing” anything in particular about geographic coordinates and CRSs. One consequence is that there is no check whether this lat/long project is applied to the proper axis of an array; it is up to the application (usually: petascope) to handle axis semantics.

One consequence is that there is no check whether this lat/long project is applied to the proper axis of an array; it is up to the application (usually: petascope) to handle axis semantics.

4.11.3. Clipping Operations

Clipping is a general operation covering polygon clipping, linestring selection, polytope clipping, curtain queries, and corridor queries. Presently, all operations are available in rasdaman via the clip function.

Further examples of clipping can be found in the systemtest for clipping.

Polygons

Syntax

select clip( c, polygon(( list of WKT points )) )
from coll as c

The input consists of an MDD expression and a list of WKT points, which determines the set of vertices of the polygon. Polygons are assumed to be closed with positive area, so the first vertex need not be repeated at the end, but there is no problem if it is. The algorithms used support polygons with self-intersection and vertex re-visitation.

Polygons may have interiors defined, such as

polygon( ( 0 0, 9 0, 9 9, 0 9, 0 0),
         ( 3 3, 7 3, 7 7, 3 7, 3 3 ) )

which would describe the annular region of the box [0:9,0:9] with the interior box [3:7,3:7] removed. In this case, the interior polygons (there may be many, as it forms a list) must not intersect the exterior polygon.

Return type

The output of a polygon query is a new array with dimensions corresponding to the bounding box of the polygon vertices, and further restricted to the collection’s spatial domain. The data in the array consists of null values where cells lie outside the polygon (or 0 values if no null values are associated with the array) and otherwise consists of the data in the collection where the corresponding cells lie inside the polygon. This could change the null values stored outside the polygon from one null value to another null value, in case a range of null values is used. By default, the first available null value will be utilized for the complement of the polygon.

An illustrative example of a polygon clipping is the right triangle with vertices located at (0,0,0), (0,10,0) and (0,10,10), which can be selected via the following query:

select clip( c, polygon((0 0 0, 0 10 0, 0 10 10)) )
from coll as c

Oblique polygons with subspacing

In case all the points in a polygon are coplanar, in some MDD object d of higher dimension than 2, users can first perform a subspace operation on d which selects the 2-D oblique subspace of d containing the polygon. For example, if the polygon is the triangle polygon((0 0 0, 1 1 1, 0 1 1, 0 0 0)), this triangle can be selected via the following query:

select clip( subspace(d, (0 0 0, 1 1 1, 0 1 1) ),
             polygon(( 0 0, 1 1 , 0 1 , 0 0)) )
from coll as d

where the result of subspace(d) is used as the domain of the polygon. For more information look in Subspace Queries.

Linestrings

Syntax

select clip( c, linestring( list of WKT points ) ) [ with coordinates ]
from coll as c

The input parameter c refers to an MDD expression of dimension equal to the dimension of the points in the list of WKT points. The list of WKT points consists of parameters such as linestring(0 0, 19 -3, 19 -21), which would describe the 3 endpoints of 2 line segments sharing an endpoint at 19 -3, in this case.

Return type

The output consists of a 1-D MDD object consisting of the points selected along the path drawn out by the linestring. The points are selected using a Bresenham Line Drawing algorithm which passes through the spatial domain in the MDD expression c, and selects values from the stored object. In case the linestring spends some time outside the spatial domain of c, the first null value will be used to fill the result of the linestring, just as in polygon clipping.

When with coordinates is specified, in addition to the original cell values the coordinate values are also added to the result MDD. The result cell type for clipped MDD of dimension N will be composite of the following form:

1. If the original cell type elemtype is non-composite:

   { long d1, ..., long dN, elemtype value }
   

2. Otherwise, if the original cell type is composite of M bands:

   { long d1, ..., long dN, elemtype1 elemname1, ..., elemetypeM elemnameM }
   

Example

Select a Linestring from rgb data with coordinates. First two values of each cell in the result are the x/y coordinates, with following values (three in this case for RGB data) are the cell values of the clip operation to which with coordinates is applied.

select encode(
    clip( c, linestring(0 19, 19 24, 12 17) ) with coordinates, "json")
from rgb as c

Result:

["0 19 119 208 248","1 19 119 208 248","2 20 119 208 248", ...]

The same query without specifying with coordinates:

select encode(
    clip( c, linestring(0 19, 19 24, 12 17) ), "json")
from rgb as c

results in

["119 208 248","119 208 248","119 208 248", ...]

Curtains

Syntax

select clip( c, curtain( projection(dimension pair),
                         polygon(( ... )) ) )
from coll as c

and

select clip( c, curtain( projection(dimension list),
                         linestring( ... ) ) )
from coll as c

The input in both variants consists of a dimension list corresponding to the dimensions in which the geometric object, either the polygon or the linestring, is defined. The geometry object is defined as per the above descriptions; however, the following caveat applies: the spatial domain of the mdd expression is projected along the projection dimensions in the projection(dimension list). For a polygon clipping, which is 2-D, the dimension list is a pair of values such as projection(0, 2) which would define a polygon in the axial dimensions of 0 and 2 of the MDD expression c. For instance, if the spatial domain of c is [0:99,0:199,0:255], then this would mean the domain upon which the polygon is defined would be [0:99,0:255].

Return type

The output consists of a polygon clipping at every slice of the spatial domain of c. For instance, if the projection dimensions of (0, 2) are used for the same spatial domain of c above, then a polygon clipping is performed at every slice of c of the form [0:99,x,0:255] and appended to the result MDD object, where there is a slice for each value of x in [0:199].

Corridors

Syntax

select clip( c, corridor( projection(dimension pair),
                          linestring( ... ),
                          polygon(( ... )) ) )
from coll as c

and

select clip( c, corridor( projection(dimension pair),
                          linestring( ... ),
                          polygon(( ... )),
                          discrete ) )
from coll as c

The input consists of a dimension list corresponding to the dimensions in which the geometric object, in this case a polygon, is defined. The linestring specifies the path along which this geometric object is integrated. One slice is sampled at every point, and at least the first point of the linestring should be contained within the polygon to ensure a meaningful result (an error is thrown in case it is not). There is an optional discrete flag which modifies the output by skipping the extrapolation of the linestring data to interior points.

Return type

The output consists of a polygon clipping at every slice of the spatial domain of c translated along the points in the linestring, where the first axis of the result is indexed by the linestring points and the latter axes are indexed by the mask dimensions (in this case, the convex hull of the polygon). The projection dimensions are otherwise handled as in curtains; it is the spatial offsets given by the linestring coordinates which impact the changes in the result. In the case where the discrete parameter was utilized, the output is indexed by the number of points in the linestring description in the query and not by the extrapolated linestring, which uses a Bresenham algorithm to find the grid points in between.

Subspace Queries

Here we cover the details of subspace queries in rasdaman. Much like slicing via a query such as

select c[0:9,1,0:9] from collection as c

the subspace query parameter allows users to extract a lower-dimensional dataset from an existing collection. It is capable of everything that a slicing query is capable of, and more. The limitation of slicing is that the selected data must lie either parallel or perpendicular to existing axes; however, with subspacing, users can arbitrarily rotate the axes of interest to select data in an oblique fashion. This control is exercised by defining an affine subspace from a list of vertices lying in the datacube. Rasdaman takes these points and finds the unique lowest-dimensional affine subspace containing them, and outputs the data closest to this slice, contained in the bounding box of the given points, into the resulting array.

Structure of the query:

select clip( c, subspace(list of WKT points) )
from coll as c

We can illustrate the usage with an example of two queries which are identical in output:

select clip( c, subspace(0 0 0, 1 0 0, 0 0 1) ) from coll as c

select c[0:1,0,0:1] from coll as c

This example will result in 1D array of sdom [0:99]:

select clip( c, subspace(19 0, 0 99) ) from test_rgb as c

This example will result in a a 2D array of sdom [0:7,0:19]:

select clip( c, subspace(0 0 0, 0 19 0, 7 0 7) )
from test_grey3d as c

and it will consist of the best integer lattice points reachable by the vectors (1,0,1) and (0,1,0) within the bounding box domain of [0:7,0:19,0:7] in test_grey3d.

Generally speaking, rasdaman uses the 1st point as a basepoint for an affine subspace containing all given points, constructs a system of equations to determine whether or not a point is in that subspace or not, and then searches the bounding box of the given points for solutions to the projection operator which maps [0:7,0:19,0:7] to [0:7,0:19]. The result dimensions are chosen such that each search yields a unique real solution, and then rasdaman rounds to the nearest integer cell before adding the value stored in that cell to the result object.

Some mathematical edge cases:

Because of arithmetic on affine subspaces, the following two queries are fundamentally identical to rasdaman:

select clip( c, subspace(0 0 0, 1 1 0, 0 1 0) )
from test_grey3d as c

select clip( c, subspace(0 0 0, 1 0 0, 0 1 0) )
from test_grey3d as c

Rasdaman’s convention is to use the first point as the translation point, and constructs the vectors generating the subspace from the differences. There is no particular reason not to use another point in the WKT list; however, knowing this, users should be aware that affine subspaces differ slightly from vector subspaces in that the following two queries differ:

select clip( c, subspace(10 10 10, 0 0 10, 10 0 10) )
from test_grey3d as c

select clip( c, subspace(0 0 0, 10 10 0, 0 10 0) )
from test_grey3d as c

The two queries have the same result domains of [0:10,0:10], and the projection for both lie on the first 2 coordinate axes since the 3rd coordinate remains constant; however, the data selections differ because the subspaces generated by these differ, even though the generating vectors of (1 1 0) and (0 1 0) are the same.

Even though the bounding box where one searches for solutions is the same between these two queries, there is no way to reach the origin with the vectors (1 1 0) and (0 1 0) starting at the base point of (10 10 10) because neither vector can impact the 3rd coordinate value of 10; similarly, starting at (0 0 0) must leave the third coordinate fixed at 0. There is nothing special about choosing the first coordinate as our base point – the numbers might change, but the resulting data selections in both queries would remain constant.

The following two queries generate the same subspace, but the latter has a larger output domain:

select clip( c, subspace(0 0 0, 1 1 0, 0 1 0) )
from test_grey3d as c

select clip( c, subspace(0 0 0, 1 1 0, 0 1 0, 0 0 0, 1 2 0) )
from test_grey3d as c

As much redundancy as possible is annihilated during a preprocessing stage which uses a Gram-Schmidt procedure to excise extraneous data ingested during query time, and with this algorithm, rasdaman is able to determine the correct dimension of the output domain.

Some algorithmic caveats:

The complexity of searching for a solution for each result cell is related to the codimension of the affine subspace, and not the dimension of the affine subspace itself. In fact, if k is the difference between the dimension of the collection array and the dimension of the result array, then each cell is determined in O(k^2) time. Preprocessing happens once for the entire query, and occurs in O(k^3) time. There is one exception to the codimensionality considerations: a 1-D affine subspace (also known as a line segment) is selected using a multidimensional generalization of the Bresenham Line Algorithm, and so the results are determined in O(n) time, where n is the dimension of the collection.

Tip: If you want a slice which is parallel to axes, then you are better off using the classic slicing style of:

select c[0:19,0:7,0] from collection as c

as the memory offset computations are performed much more efficiently.

4.11.4. Induced Operations

Induced operations allow to simultaneously apply a function originally working on a single cell value to all cells of an MDD. The result MDD has the same spatial domain, but can change its base type.

Examples

img.green + 5 c

This expression selects component named “green” from an RGB image and adds 5 (of type char, i.e., 8 bit) to every pixel.

img1 + img2

This performs pixelwise addition of two images (which must be of equal spatial domain).

Induction and structs

Whenever induced operations are applied to a composite cell structure (“structs” in C/C++), then the induced operation is executed on every structure component. If some cell structure component turns out to be of an incompatible type, then the operation as a whole aborts with an error.

For example, a constant can be added simultaneously to all components of an RGB image:

select rgb + 5
from rgb

Induction and complex

Complex numbers, which actually form a composite type supported as a base type, can be accessed with the record component names re and im for the real and the imaginary part, resp.

Example

The first expression below extracts the real component, the second one the imaginary part from a complex number c:

c.re
c.im

Unary Induction

Unary induction means that only one array operand is involved in the expression. Two situations can occur: Either the operation is unary by nature (such as boolean not); then, this operation is applied to each array cell. Or the induce operation combines a single value (scalar) with the array; then, the contents of each cell is combined with the scalar value.

A special case, syntactically, is the struct component selection (see next subsection).

In any case, sequence of iteration through the array for cell inspection is chosen by the database server (which heavily uses reordering for query optimisation) and not known to the user.

Syntax

mddExp binaryOp scalarExp
scalarExp binaryOp mddExp
unaryOp mddExp

Example

The red images of collection rgb with all pixel values multiplied by 2:

select rgb.red * 2c
from rgb

Note that the constant is marked as being of type char so that the result of the two char types again will yield a char result (8 bit per pixel). Omitting the “c” would lead to an addition of long integer and char, the result being long integer with 32 bit per pixel. Although pixel values obviously are the same in both cases, the second alternative requires four times the memory space.

Struct Component Selection

Component selection from a composite value is done with the dot operator well-known from programming languages. The argument can either be a number (starting with 0) or the struct element name. Both statements of the following example would select the green plane of the sample RGB image.

This is a special case of a unary induced operator.

Syntax

mddExp.attrName
mddExp.intExp

Examples

select rgb.green
from rgb

select rgb.1
from rgb

Figure 4.10 RGB image and green component

Note

Aside of operations involving base types such as integer and boolean, combination of complex base types (structs) with scalar values are supported. In this case, the operation is applied to each element of the structure in turn. Both operands then have to be of exactly the same type, which further must be the same for all components of the struct.

Examples

The following expression reduces contrast of a color image in its red, green, and blue channel simultaneously:

select rgb / 2c
from rgb

An advanced example is to use image properties for masking areas in this image. In the query below, this is done by searching pixels which are “sufficiently green” by imposing a lower bound on the green intensity and upper bounds on the red and blue intensity. The resulting boolean matrix is multiplied with the original image (i.e., componentwise with the red, green, and blue pixel component); the final image, then, shows the original pixel value where green prevails and is {0,0,0} (i.e., black) otherwise (Figure 4.11)

select rgb * ( (rgb.green > 130c) and
               (rgb.red   < 110c) and
               (rgb.blue  < 140c) )
from rgb

Figure 4.11 Suppressing “non-green” areas

Note

This mixing of boolean and integer is possible because the usual C/C++ interpretation of true as 1 and false as 0 is supported by rasql.

Binary Induction

Binary induction means that two arrays are combined.

Syntax

mddExp binaryOp mddExp

Example

The difference between the images in the mr collection and the image in the mr2 collection:

select mr - mr2
from mr, mr2

Note

As in the previous section, two cases have to be distinguished:

• Both left hand array expression and right hand array expression operate on the same array, for example:

  select rgb.red - rgb.green
  from rgb
  

  In this case, the expression is evaluated by combining, for each coordinate position, the respective cell values from the left hand and right hand side.

• Left hand array expression and right hand array expression operate on different arrays, for example:

  select mr - mr2
  from mr, mr2
  

  This situation specifies a cross product between the two collections involved. During evaluation, each array from the first collection is combined with each member of the second collection. Every such pair of arrays then is processed as described above.

Obviously the second case can become computationally very expensive, depending on the size of the collections involved - if the two collections contain n and m members, resp., then n*m combinations have to be evaluated.

Case statement

The rasdaman case statement serves to model n-fold case distinctions based on the SQL92 CASE statement which essentially represents a list of IF-THEN statements evaluated sequentially until either a condition fires and delivers the corresponding result or the (mandatory) ELSE alternative is returned.

In the simplest form, the case statement looks at a variable and compares it to different alternatives for finding out what to deliver. The more involved version allows general predicates in the condition.

This functionality is implemented in rasdaman on both scalars (where it resembles SQL) and on MDD objects (where it establishes an induced operation). Due to the construction of the rasql syntax, the distinction between scalar and induced operations is not reflected explicitly in the syntax, making query writing simpler.

Syntax

• Variable-based variant:

  case generalExp
  when scalarExp then generalExp
  ...
  else generalExp
  end
  

  All generalExps must be of a compatible type.

• Expression-based variant:

  case
  when booleanExp then generalExp
  ...
  else generalExp
  end
  

All generalExp’s must be evaluate to a compatible type.

Example

Traffic light classification of an array object can be done as follows.

select
  case
  when mr > 150 then { 255c, 0c, 0c }
  when mr > 100 then { 0c, 255c, 0c }
  else               { 0c, 0c, 255c }
  end
from mr

This is equivalent to the following query; note that this query is less efficient due to the increased number of operations to be evaluated, the expensive multiplications, etc:

select
  (mr > 150)                { 255c, 0c, 0c }
+ (mr <= 150 and mr > 100)  { 0c, 255c, 0c }
+ (mr <= 100)               { 0c, 0c, 255c }
from mr

Restrictions

In the current version, all MDD objects participating in a case statement must have the same tiling. Note that this limitation can often be overcome by factoring divergingly tiled arrays out of a query, or by resorting to the query equivalent in the above example using multiplication and addition.

Induction: All Operations

Below is a complete listing of all cell level operations that can be induced, both unary and binary.

If two different data types are involved, the result will be of the more general type; e.g., float and integer addition will yield a float result.

is, and, or, xor, not

For each cell within some Boolean MDD (or evaluated MDD expression), combine it with the second MDD argument using the logical operation and, or, or xor. The is operation is equivalent to = (see below). The signature of the binary induced operation is

is, and, or, xor: mddExp, intExp -> mddExp

Unary function not negates each cell value in the MDD.

+, -, *, /

For each cell within some MDD value (or evaluated MDD expression), add it with the corresponding cell of the second MDD parameter. For example, this code adds two (equally sized) images:

img1 + img2

As usual, these arithmetic operations are overloaded to expect mddExp as well as numExp, integer as well as float numbers, and single precision as well as double precision values.

In a division, if at least one cell in the second MDD parameter is zero then an exception will be thrown.

=, <, >, <=, >=, !=

For two MDD values (or evaluated MDD expressions), compare for each coordinate the corresponding cells to obtain the Boolean result indicated by the operation.

These comparison operators work on all atomic cell types.

On composite cells, only = and != are supported; both operands must have a compatible cell structure. In this case, the comparison result is the conjunction (“and” connection) of the pairwise comparison of all cell components.

min, max

For two MDD values (or evaluated MDD expressions), take the minimum / maximum for each pair of corresponding cell values in the MDDs.

Example:

a min b

For struct valued MDD values, struct components in the MDD operands must be pairwise compatible; comparison is done in lexicographic order with the first struct component being most significant and the last component being least significant.

bit(mdd, pos)

For each cell within MDD value (or evaluated MDD expression) mdd, take the bit with nonnegative position number pos and put it as a Boolean value into a byte. Position counting starts with 0 and runs from least to most significant bit. The bit operation signature is

bit: mddExp, intExp -> mddExp

In C/C++ style,

bit(mdd,pos)

is equivalent to

mdd >> pos & 1

overlay

The overlay operator allows to combine two equally sized MDDs by placing the second one “on top” of the first one, informally speaking. Formally, overlaying is done in the following way:

• wherever the second operand’s cell value is non-zero [7], the result value will be this value.
• wherever the second operand’s cell value is zero, the first argument’s cell value will be taken.

This way stacking of layers can be accomplished, e.g., in geographic applications. Consider the following example:

ortho overlay tk.water overlay tk.streets

When displayed the resulting image will have streets on top, followed by water, and at the bottom there is the ortho photo.

Strictly speaking, the overlay operator is not atomic. Expression

a overlay b

is equivalent to

(b != 0) * b + (b = 0) * a

However, on the server the overlay operator is executed more efficiently than the above expression.

Arithmetic, trigonometric, and exponential functions

The following advanced arithmetic functions are available with the obvious meaning, each of them accepting an MDD object:

abs()
sqrt()
exp() log() ln() pow() power()
sin() cos() tan()
sinh() cosh() tanh()
arcsin() arccos() arctan()

pow, power

The power function can be written as pow() and power(), both are identical. The signature is:

power( base, exp )

where base is an MDD and exp is a floating point number.

Exceptions

If at least one cell in the base argument violates the usual constraints on such functions (such as a zero value as input for log()) then an exception will be thrown.

cast

Sometimes the desired ultimate scalar type or MDD cell type is different from what the MDD expression would suggest. To this end, the result type can be enforced explicitly through the cast operator.

The syntax is:

(newType) generalExp

where newType is the desired result type of expression generalExp.

Like in programming languages, the cast operator converts the result to the desired type if this is possible at all. For example, the following scalar expression, without cast, would return a double precision float value; the cast makes it a single precision value:

(float) avg_cells( mr )

Both scalar values and MDD can be cast; in the latter case, the cast operator is applied to each cell of the MDD yielding an array over the indicated type.

The cast operator also works properly on recursively nested cell structures. In such a case, the cast type is applied to every component of the cell. For example, the following expression converts the pixel type of an (3x8 bit) RGB image to an image where each cell is a structure with three long components:

(long) rgb

Obviously in the result structure all components will bear the same type.

Restrictions

Currently only base types are permitted as cast result types, it is not possible to cast to a struct or complex type, e.g.

(RGBPixel) rgb -- illegal

On base type complex, only the following operations are available right now:

+ - * /

4.11.5. Scaling

Shorthand functions are available to scale multidimensional objects. They receive an array as parameter, plus a scale indicator. In the most common case, the scaling factor is an integer or float number. This factor then is applied to all dimensions homogeneously. For a scaling with individual factors for each dimension, a scaling vector can be supplied which, for each dimension, contains the resp. scale factor. Alternatively, a target domain can be specified to which the object gets scaled.

Syntax

scale( mddExp, intExp )
scale( mddExp, floatExp )
scale( mddExp, intVector )
scale( mddExp, mintervalExp )

Examples

The following example returns all images of collection mr where each image has been scaled down by a factor of 2.

select scale( mr, 0.5 )
from mr

Next, mr images are enlarged by 4 in the first dimension and 3 in the second dimension:

select scale( mr, [ 4, 3 ] )
from mr

In the final example, mr images are scaled to obtain 100x100 thumbnails (note that this can break aspect ratio):

select scale( mr, [ 0:99, 0:99 ] )
from mr

Note

Function scale() breaks tile streaming, it needs to load all tiles affected into server main memory. In other words, the source argument of the function must fit into server main memory. Consequently, it is not advisable to use this function on very large items.

Note

Currently only nearest neighbour interpolation is supported for scaling.

4.11.6. Concatenation

Concatenation of two arrays “glues” together arrays by lining them up along an axis.

This can be achieved with a shorthand function, concat, which for convenience is implemented as an n-ary operator accepting an unlimited number of arrays. The operator takes the input arrays, lines them up along the concatenation dimension specified in the request, and outputs one result array. To this end, each input array is shifted to the appropriate position, with the first array’s position remaining unchanged; therefore, it is irrelevant whether array extents, along the concatenation dimension, are disjoint, overlapping, or containing each other.

The resulting array’s dimensionality is equal to the input array dimensionality.

The resulting array extent is the sum of all extents along the concatenation dimension, and the extent of the input arrays in all other dimensions.

The resulting array cell type is the largest type covering all input array cell types (type coercion).

Constraints

All participating arrays must have the same number of dimensions.

All participating arrays must have identical extents in all dimensions, except that dimension along which concatenation is performed.

Input array data types must be compatible.

Syntax

concat mddExp with mddExp ... with mddExp along integer

Examples

The following query returns the concatenation of all images of collection mr with themselves along the first dimension (Figure 4.12).

select concat mr with mr along 0
from mr

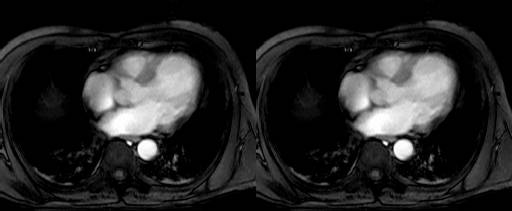
Figure 4.12 Query result of single concatenation

The next example returns a 2x2 arrangement of images (Figure 4.13):

select concat (concat mr with mr along 0)
with (concat mr with mr along 0)
along 1
from mr

Figure 4.13 Query result of multiple concatenation

4.11.7. Quantiles [RE]

Overview

The rasql enterprise function quantile() delivers the q-quantile distribution over a given array object.

Quantiles (cf. Wikipedia) are “points taken at regular intervals from the cumulative distribution function (CDF) of a random variable. Dividing ordered data into q essentially equal- sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets. Put another way, the k-th q-quantile for a random variable is the value x such that the probability that the random variable will be less than x is at most k/q and the probability that the random variable will be more than x is at most (q - k) / q = 1 - (k / q). There are q-1 of the q-quantiles, one for each integer k satisfying 0 < k < q.”

The quantile() Function

The quantile() function signature is

quantile: mddExpr, intExpr -> mddExpr

Given an MDD object M and a parameter Q, the quantile function sorts the data in increasing order, partitions the data in Q equal parts, and returns a 1-dimensional MDD object of size Q-1 and same type as the input object, which contains the boundary values between the consecutive parts.

Example

Assume an n-D MDD, M, of which we want to have all 100-quantiles (percentiles); this is written as

quantile(M, 100)

This expression results in a 1-D object containing 99 values, where the first value corresponds to the 1st percentile:

quantile(M, 100)[0]

and the 50th value to the 50th percentile:

quantile(M, 50)[49]

Since the 50th percentile is equivalent to the median (2-quantile), the above query is equivalent to

quantile(M, 2)[0]

Quantile Fields

The quantile function can be used to derive quantile fields. For example, assume an x/y/t time series object T where x, y, and t have dimensions 0, 1, and 2, resp. The following expression obtains an x/y map of 95% percentiles (q=100) over time for each x/y location, thereby detecting anomalies over time:

marray x in sdom(T)[0], y in sdom(T)[1]
values quantile( T[ x, y ], 100)[94]

Limitations

Only arrays with an atomic cell type are supported currently.

Sorting of data is done in main memory so the size of a single quantile result array is limited to the server’s main memory.

4.11.8. Condensers

Frequently summary information of some kind is required about some array, such as sum or average of cell values. To accomplish this, rasql provides the concept of condensers.

A condense operation (or short: condenser) takes an array and summarizes its values using a summarization function, either to a scalar value (e.g. computing the sum of all its cells), or to another array (e.g. summarizing a 3-D cube into a 2-D image by adding all the horizontal slices that the cube is composed of).

A number of condensers is provided as rasql built-in functions.

• For numeric arrays, add_cells() delivers the sum and avg_cells() the average of all cell values. Operators min_cells() and max_cells() return the minimum and maximum, resp., of all cell values in the argument array. stddev_pop, stddev_samp, var_pop, and var_samp allow to calculate the population and sample standard deviation, as well as the population and sample variance of the MDD cells.
• For boolean arrays, the condenser count_cells() counts the cells containing true; some_cells() operation returns true if at least one cell of the boolean MDD is true, all_cells() returns true if all of the MDD cells contain true as value.

Please keep in mind that, depending on their nature, operations take a boolean, numeric, or arbitrary mddExp as argument.

Syntax

count_cells( mddExp )
add_cells( mddExp )
avg_cells( mddExp )
min_cells( mddExp )
max_cells( mddExp )
some_cells( mddExp )
all_cells( mddExp )
stddev_pop( mddExp )
stddev_samp( mddExp )
var_pop( mddExp )
var_samp( mddExp )

Examples

The following example returns all images of collection mr where all pixel values are greater than 20. Note that the induction “>20” generates a boolean array which, then, can be collapsed into a single boolean value by the condenser.

select mr
from mr
where all_cells( mr > 20 )

The next example selects all images of collection mr with at least one pixel value greater than 250 in region [ 120:160, 55:75] (Figure 4.14).

select mr
from mr
where some_cells( mr[120 : 160, 55 : 75] > 250 )

Figure 4.14 Query result of specific selection

Finally, this query calculates the sample variance of mr2:

select var_samp( mr2 ) from mr2

4.11.9. General Array Condenser

All the condensers introduced above are special cases of a general principle which is represented by the general condenser statement.

The general condense operation consolidates cell values of a multidimensional array to a scalar value based on the condensing operation indicated. It iterates over a spatial domain while combining the result values of the cellExps through the condenserFunction indicated.

The general condense operation consolidates cell values of a multidimensional array to a scalar value or an array, based on the condensing operation indicated.

Condensers are heavily used in two situations:

• To collapse boolean arrays into scalar boolean values so that they can be used in the where clause.
• In conjunction with the marray constructor (see next section) to phrase high-level signal processing and statistical operations.

Syntax

condense condenserOp
over var in mintervalExp
using cellExp

condense condenserOp
over var in mintervalExp
where booleanExp
using cellExp

The mintervalExp terms together span a multidimensional spatial domain over which the condenser iterates. It visits each point in this space exactly once, assigns the point’s respective coordinates to the var variables and evaluates cellExp for the current point. The result values are combined using condensing function condenserOp. Optionally, points used for the aggregate can be filtered through a booleanExp; in this case, cellExp will be evaluated only for those points where booleanExp is true, all others will not be regarded. Both booleanExp and cellExp can contain occurrences of variables pointVar.

Examples

This expression below returns a scalar representing the sum of all array values, multiplied by 2 (effectively, this is equivalent to add_cells(2*a)):

condense +
over x in sdom(a)
using 2 * a[ x ]

The following expression returns a 2-D array where cell values of 3-D array a are added up along the third axis:

condense +
over x in [0:100]
using a[ *:*, *:*, x[0] ]

Note that the addition is induced as the result type of the value clause is an array. This type of operation is frequent, for example, in satellite image time series analysis where aggregation is performed along the time axis.

Shorthands

Definition of the specialized condensers in terms of the general condenser statement is as shown in Table 4.4.

Table 4.4 Specialized condensers; a is a numeric, b a boolean array.

Aggregation definition	Meaning
add_cells(a) = condense + over x in sdom(a) using a[x]	sum over all cells in a
avg_cells(a) = sum_cells(a) / card(sdom(a))	Average of all cells in a
min_cells(a) = condense min over x in sdom(a) using a [x]	Minimum of all cells in a
max_cells(a) = condense max over x in sdom(a) using a[x]	Maximum of all cells in a
count_cells(b) = condense + over x in sdom(b) where b[x] != 0 using 1	Number of cells in b which are non-zero / not false
some_cells(b) = condense or over x in sdom(b) using b[x]	is there any cell in b with value true?
all_cells(b) = condense and over x in sdom(b) using b[x]	do all cells of b have value true?

Restriction

Currently condensers of any kind over cells of type complex are not supported.

4.11.10. General Array Constructor

The marray constructor allows to create n-dimensional arrays with their content defined by a general expression. This is useful

• whenever the array is too large to be described as a constant (see Array Constants) or
• when the array’s cell values are derived from some other source, e.g., for a histogram computation (see examples below).

Syntax

The basic shape of the marray construct is as follows.

marray var in mintervalExp [, var in mintervalExp]
values cellExp

Iterator Variable Declaration

First, the constructor allocates an array in the server with the spatial domain defined by the cross product of all mintervalExp. For example, the following defines a 2-D 5x10 matrix:

marray x in [1:5], y in [1:10]
values ...

The base type of the array is determined by the type of cellExp. Variable var can be of any number of dimensions.

Iteration Expression

In the second step, the constructor iterates over the spatial domain defined as described, successively evaluating cellExp for each variable combination; the result value is assigned to the cell with the coordinate currently under evaluation. To this end, cellExp can contain arbitrary occurrences of var. The cellExp must evaluate to a scalar (i.e., a single or composite value, as opposed to an array). The syntax for using a variable is:

• for a one-dimensional variable:

  var
  

• for a higher-dimensional variable:

  var [ index-expr ]
  

where index-expr is a constant expression (no sdom() etc.!) evaluating to a non-negative integer; this number indicates the variable dimension to be used.

Figure 4.15 2-D array with values derived from first coordinate

Examples

The following creates an array with spatial domain [1:100,-50:200] over cell type char, each cell being initialized to 1.

marray x in [ 1:100, -50:200 ]
values 1c

In the next expression, cell values are dependent on the first coordinate component (cf. Figure 4.15):

marray x in [ 0:255, 0:100 ]
values x[0]

The final two examples comprise a typical marray/condenser combination. The first one takes a sales table and consolidates it from days to week per product. Table structure is as given in Figure 4.16.:

select marray tab in [ 0:sdom(s)[0].hi/7, sdom(s)[1] ]
over day in [ 0:6 ]
values condense +
using s[ day[0] + tab7 ] , tab[1] ]
from salestable as s

The last example computes histograms for the mr images. The query creates a 1-D array ranging from 0 to 9 where each cell contains the number of pixels in the image having the respective intensity value.

select marray v in [ 0 : 9 ]
values condense +
over x in sdom(mr)
where mr[x] = v[0]
using 1
from mr

Figure 4.16 Sales table consolidation

Shorthand

As a shorthand, variable var can be used without indexing; this is equivalent to var[0]:

marray x in [1:5]
values a[ x ]       -- equivalent to a[ x[0] ]

Many vs. One Variable

Obviously an expression containing several 1-D variables, such as:

marray x in [1:5], y in [1:10]
values a[ x[0], y[0] ]

can always be rewritten to an equivalent expression using one higher-dimensional variable, for example:

marray xy in [1:5, 1:10]
values a[ xy[0], xy[1] ]

Iteration Sequence Undefined

The sequence in which the array cells defined by an marray construct are inspected is not defined. In fact, server optimisation will heavily make use of reordering traversal sequence to achieve best performance.

Restriction

Currently there is a restriction in variable lists: for each marray variable declaration, either there is only one variable which can be multidimensional, or there is a list of one-dimensional variables; a mixture of

case that a list of variables is defined. In this case, a variable definition can only consist of constant expressions, it is not possible, e.g., to use sdom().

A Note on Expressiveness and Performance

The general condenser and the array constructor together allow expressing a very broad range of signal processing and statistical operat­ions. In fact, all other rasql array operations can be expressed through them, as Table 4.5 exemplifies. Nevertheless, it is advisable to use the specialized operations whenever possible; not only are they more handy and easier to read, but also internally their processing has been optimized so that they execute considerably faster than the general phrasing.

Table 4.5 Phrasing of Induction, Trimming, and Section via marray

operation	shorthand	phrasing with marray
Trimming	a[ *:*, 50:100 ]	marray x in [sdom(a)[0], 50:100] values a[ x ]
Section	a[ 50, *:* ]	marray x in sdom(a)[1] values a[ 50, x ]
Induction	a + b	marray x in sdom(a) values a[x] + b[x]

4.12. Data Format Conversion

Without further indication, arrays are accepted and delivered in the client’s main memory format, regardless of the client and server architecture. Sometimes, however, it is desirable to use some data exchange format - be it because some device provides a data stream to be inserted in to the database in a particular format, or be it a Web application where particular output formats have to be used to conform with the respective standards.

To this end, rasql provides two families of operations:

• encode() for encoding an MDD in a particular data format repre­sent­at­ion; formally, the result will be a 1D byte array.
• decode() for decoding a byte stream (such as a query input parameter during insert - see examples below) into an actionable MDD.

Implementation of these functions is based on GDAL and, hence, supports all GDAL formats. Some formats are implemented in addition, see the description below.

4.12.1. Encode / Decode Operations

Syntax

encode( mddExp , formatidentifier )
encode( mddExp , formatidentifier , formatParams )

decode( mddExp )
decode( mddExp , formatidentifier, formatParams )

The encode() functions accept a format identifier in its second parameter whose values are GDAL format identifiers. The decode() function automatically detects the format used, so there is no format parameter. It accepts a format when a custom internal implementation should be selected instead of using GDAL, e.g. netCDF, GRIB, or CSV / JSON.

Examples

The following query loads a TIFF image into collection rgb:

insert into rgb
values decode( $1 )

This query extracts PNG images (one for each tuple) from collection rgb:

select encode( rgb, "png" )
from rgb

Input/Output Types

The result of any encoding function is a 1D MDD of type char holding the MDD encoded in the target format.

The input to any decoding function is such a 1D MDD, conversely.

Type Matching

For encoding an MDD into a data format (and vice versa), the MDD type must match the dimension and data type the image format can handle - it is mandatory that the array to be transformed or generated conforms to the overall structure supported by the particular data exchange format. For example, TIFF can only handle 2-D arrays with a particular subset of supported cell types.

The cell type of an MDD input stream may need to be provided explicitly through a cast operator, otherwise the query could be aborted with an error on cell type mismatch. The following query correctly inserts a TIFF image with floating-point values into collection Bathymetry:

insert into Bathymetry
values (double) decode( $1 )

The reason for this requirement is that, at the time the query is analyzed, the input parameters are not yet decoded, this takes place at a later stage. Hence, the server has no knowledge about the data type, and this prevents it from understanding the query correctly.

4.12.2. Formats Supported

The decode() and encode() functions utilize the open-source GDAL library for transcoding. A list of the GDAL supported formats can be obtained through gdalinfo or from www.gdal.org/formats_list.html:

$ gdalinfo -formats
Supported Formats:
  VRT (rw+v): Virtual Raster
  GTiff (rw+v): GeoTIFF
  NITF (rw+v): National Imagery Transmission Format
  RPFTOC (ro): Raster Product Format TOC format
  ...

Additionally, the following formats beyond GDAL are supported by rasdaman (more details in Multidimensional Format Support:

• CSV (comma-separated values), format name: “csv”
• JSON, format name: “json” (same as CSV, but uses [ and ] as dimension separators)
• NetCDF4 (n-D), format name “netcdf”
• HDF4 (n-D), format name “hdf”
• GRIB (n-D), format name “grib” (decode only)

4.12.3. Conversion Options

The encode() / decode() functions can be provided with a format specific parameter JSON string, formatParams, for fine-tuning the conversion. Certain parameters are common to all formats:

1. variable subset: variable names, band ids;
2. internal structure: lat/lon, x/y/t, message domains in GRIB;
3. x/y transpose: indicate if x/y should be transposed or is it not relevant (comes up in netCDF and GRIB and has a performance penalty at both decode and encode)
4. filepath: absolute path to an input file, this improves ingestion performance if the data is on the same machine as the rasdaman server, as the network transport is bypassed
5. subset domain: only the given subset needs to be extracted from the input file; note that the subset domain must match in dimensionality with the file dimensionality, and must be accordingly offset to the grid origin in the file, which is typically 0,0,0,..

Quote escaping: when used in a query the format parameters are the third argument of the decode/encode functions. They need to be in quotes, i.e. "formatParameters". Because of these outer quotes, all quotes inside of the formatParameters need to be escaped (\"). For example, "{\"transpose\": [0,1] }" is the right way to specify transposition, while "{"transpose": [0,1] }" will lead to failure.

Single line: the format parameters JSON string must be a single line when specified on the command-line.

decode

{
  // Specify variable names, band ids (0-based), etc.
  "variables": [ "var1", "var2", ... ],

  // Absolute path to input file(s). This improves ingestion performance if the data
  // is on the same machine as the rasdaman server, as the network transport is bypassed;
  // It is possible that a format could have multiple files associated to each other,
  // so this argument is an array of filepaths.
  // Note: supported for netCDF, GRIB, and GDAL formats.
  "filePaths": [ "/path/to/file.tif", ... ],

  // Only the given subset needs to be extracted from the input file.
  "subsetDomain": "[0:100,0:100]",

  // Indicate if x/y should be transposed or is it not relevant (comes up in netCDF and
  // GRIB and has a performance penalty, so avoid if possible);
  // The argument is an array of 0-based axis ids indicating the axes that need to be
  // transposed, e.g. the first axis is 0, second is 1, etc; must be contiguous, [N,N+1]
  "transpose": [ 0, 1 ],

  // Describe the internal structure of a format if necessary, e.g. message domains in GRIB
  "internalStructure": {
    "messageDomains": [
      { "msgId": 1, "domain": "[0:0,0:0,0:719,0:360]" },
      { "msgId": 2, "domain": "[0:0,1:1,0:719,0:360]" },
      { "msgId": 3, "domain": "[0:0,2:2,0:719,0:360]" },
      ...
    ]
  },

  // Extra format parameters
  "formatParameters": {
    "key": "value",
    // CSV/JSON specific (example values)
    "basetype": "struct { float f, long l }",
    "domain": "[0:100,0:100]"
  },

  // Configuration options (string key/value pairs);
  // details for GDAL: https://trac.osgeo.org/gdal/wiki/ConfigOptions
  "configOptions": {
    "GDAL_CACHEMAX": "64",
    ...
  }
}

encode

{
  // netCDF-specific
  "dimensions": [ "dimName1", "dimName2", ... ],

  // Specify variable names, band ids (0-based), etc; the variables can be objects listing
  // details like type, metadata and data for netCDF, or simply an array of variable names
  "variables": {
    "var1": {..},
    "var2": {..},
    ...
  },

  // single string, or multiple key/value pairs
  "metadata": {
    "standard_name": "sea_surface_temperature",
    "long_name": "Sea Surface Temperature",
    "units": "K"
  },

  // Indicate if x/y should be transposed or is it not relevant (comes up in netCDF and GRIB
  // and has a performance penalty, so avoid if possible);
  // The argument is an array of 0-based axis ids indicating the axes that need to be
  // transposed, e.g. the first axis is 0, second is 1, etc; must be contiguous, [N,N+1]
  "transpose": [0,1],

  // geo-referencing information, can be either given as a geo bounding box or an
  // array of GCPs (but not both); see 'Affine GeoTransform' and 'GCPs' sections
  // at http://www.gdal.org/gdal_datamodel.html
  "geoReference": {
    "crs": "EPSG:4326",

    // a geo bounding box
    "bbox": {
      "xmin": -15,
      "ymin": 0.5,
      "xmax": 10.2,
      "ymax": 25
    },

    // or an array of GCPs
    "GCPs": [
      {
        "id": ..,     // optional unique identifier (gets the array index by default)
        "info": ..,   // optional text associated with the GCP

        // these must have double value
        "pixel": .., "line": ..,     // GCP location on the raster
        "x": ..,  "y": ..,  "z": ..  // georeferenced location, with "z" being optional
                                     // (zero by default)
      }
      ...
    ]
  },

  // single value or an array of values if different for multiple bands
  // ( if nodata= 1 single value, it will be applied to all bands, and if nodata =
  // array of values then each value is applied to each band separately ).
  //
  // special floating-point constants supported (case-sensitive):
  // NaN, NaNf, Infinity, -Infinity
  "nodata": 0,

  // for more details see "Color Table" at http://www.gdal.org/gdal_datamodel.html
  "colorPalette": {
    "paletteInterp": "RGB"       // optional palette interpretation, one of
                                 // "Gray", "RGB", "CMYK", "HSL" (default: "RGB")
    // An optional array of band color interpretations, one of:
    // Undefined Gray Palette Red Green Blue Alpha Hue Saturation Lightness Cyan
    // Magenta Yellow Black YCbCr_Y YCbCr_Cb YCbCr_Cr YCbCr_Cr
    "colorInterp": [ "Red", "Green", "Blue" ]
    "colorTable": [              // optional color table, an array of arrays with 1, 3 or
                                 // 4 short values (depending on the colorInterpretation)
      [255, 0, 0, 0],            // for each color entry; pixels with value 0 are colored red
      ...
    ]
  },

  // Format dependent extra parameters, e.g. gdal specific format parameters
  "formatParameters": {
    "INTERLEAVE": "BAND",
    "COMPRESSION": "LZW",
    // CSV/JSON specific
    "order": "inner_outer",
    ...
  },

  // Configuration options (string key/value pairs);
  // details for GDAL: https://trac.osgeo.org/gdal/wiki/ConfigOptions
  "configOptions": {
    "GDAL_CACHEMAX": "64",
    ...
  }
}

GDAL Format Parameters

The key/values under "formatParameters" are passed onto GDAL as given. Each format supports specific parameters as documented on the GDAL formats page <https://www.gdal.org/formats_list.html>.

Rasdaman itself does not change the default values for these parameters, with the following exceptions:

• PNG - the compression level when encoding to PNG (option ZLEVEL) will be set to 2 if the user does not specify it explicitly and the result array is not of type boolean. The default compression level of 6 does not offer considerable space savings on typical image results (e.g. around 10% lower file size for satellite image), while significantly increasing the time to encode, taking up to 3-5x longer.

Examples

1. Using filePaths in JSON format (<[0:0] 1c> is a dummy array value which is mandatory):

   UPDATE test_mr SET test_mr[0:255,0:210] ASSIGN decode(<[0:0] 1c>, "GDAL",
       "{\"filePaths\":[\"/home/rasdaman/mr_1.png\"]}") WHERE oid(test_mr) = 6145
   

2. Transpose the last two axes of the output before encoding to PNG:

   select encode(c, "png", "{ \"transpose\": [0,1] }") from mr2 as c
   

3. Add some global attribute as metadata in netcdf:

   select encode(c, "netcdf", "{ \"transpose\": [1,0], \"nodata\": [100, 200, 260],
       \"metadata\": { \"new_metadata\": \"This is a new added metadata\" },
       \"formatParameters\": {\"INTERLEAVE\": \"BAND\"},
       \"configOptions\": { \"GDAL_CACHEMAX\": \"64\"} }")
   from test_mean_summer_airtemp as c
   

(Deprecated) Key-Value Conversion Options

The optional string parameter allows passing format-specific options, as well as generic parameters, like a geo-referencing bounding box and CRS. All parameter settings are concatenated into one quoted string of the following format:

"key1=value1;key2=value2;..."

Both key and value are case-sensitive.

In addition to format specific parameters, most formats recognize the following parameters:

• xmin, ymin, xmax, ymax for specifying the bounding box;

• a general metadata string to be placed into the output file (if the format supports this);

• nodata allows a list of null values for each band. If only one value is provided it applies to all bands simultaneously; alternatively, a comma-separated list of null values can be provided individually per band. For example, the following will set blue to transparent:

  "nodata=0,0,255;"
  

• crs for indicating the Coordinate Reference System (CRS) in which the above coordinates are expressed. Any of these CRS representations is accepted:

• Well Known Text (as per GDAL)

• “EPSG:n”

• “EPSGA:n”

• “AUTO:proj_id,unit_id,lon0,lat0” indicating OGC WMS auto projections

• “urn:ogc:def:crs:EPSG::n” indicating OGC URNs (deprecated by OGC)

• PROJ.4 definitions

• well known names, such as NAD27, NAD83, WGS84 or WGS72.

• WKT in ESRI format, prefixed with “ESRI::”

• “IGNF:xxx” and “+init=IGNF:xxx”, etc.

Since recently (v1.10), GDAL also supports OGC CRS URLs, OGC’s preferred way of identifying CRSs.

4.12.4. Multidimensional Format Support

Here we cover the formats with native support in rasdaman.

NetCDF

TODO

GRIB

TODO

CSV/JSON

The CSV format is an ASCII character string where the cell values are represented by numbers linearized in row-major order. Row and column delimiters may be used, { and } for CSV, [ and ] for JSON. The delimiters are optional when decoding data in this format.

decode()

Numbers from the input file are read in order of appearance and stored without any reordering in rasdaman; whitespace plus the following characters are ignored:

'{', '}', ',', '"', '\'', '(', ')', '[', ']'

Mandatory extra parameters:

domain

Domain d has to match number of cells read from input file. E.g. for \"domain\": \"[1:5, 0:10, 2:3]\", there should be 110 numbers in the input file.

basetype

Atomic or struct base type; named structs like RGBPixel are not supported. Examples:

long
char
struct { char red, char blue, char green }

Examples

Assume array A is a 2x3 array of longs given as a string as follows:

1,2,3,2,1,3

Inserting A into rasdaman can be done with

insert into A
values decode($1, "csv", "{ \"formatParameters\":
                            { \"domain\": \"[0:1,0:2]\",
                              \"basetype\": \"long\" } }")

Further, let B be an 1x2 array of RGB values given as follows:

{1,2,3},{2,1,3}

Inserting B into rasdaman can be done by passing it to this query:

insert into B
values decode( $1, "csv", "{ \"formatParameters\":
                            { \"domain\": \"[0:0,0:1]\",
                              \"basetype\": \"struct{char red,
                                                     char blue,
                                                     char green}\" } }")

B could just as well be formatted like this with the same effect (note the line break):

1 2 3
2 1 3

encode()

Data encoded with CSV is a comma-separated list of values, such that each row of values (for every dimension, not just the last one) is between { and } braces ([ and ] for JSON). Composite cells are output as space separated values in quotes.

The array serialization order can be specified with an optional format parameter order, which can be outer_inner (default, last dimension iterates fastest), or vice-versa, inner_outer.

Examples

Suppose we have array A = <[0:1,0:1] 0, 1; 2, 3>. Encoding to CSV by default

select encode(A, "csv") from A

will result in the following output:

{{0, 1}, {2, 3}}

while encoding to JSON with:

select encode(A, "json") from A

will result in the following output:

[[0, 1], [2, 3]]

Specifying inner_outer order with

select encode(A, "csv", "{ \"formatParameters\":
                           { \"order\": \"inner_outer\" } }") from A

will result in the following output (left-most dimensions iterate fastest):

{{0, 2}, {1, 3}}

Let B be an RGB array <[0:0,0:1] {0c, 1c, 2c}, {3c, 4c, 5c}>. Encoding it to CSV with default order will result in the following output:

{“0 1 2”,”3 4 5”}

4.13. Object identifiers

Function oid() gives access to an array’s object identifier (OID). It returns the local OID of the database array. The input parameter must be a variable associated with a collection, it cannot be an array expression. The reason is that oid() can be applied to only to persistent arrays which are stored in the database; it cannot be applied to query result arrays - these are not stored in the database, hence do not have an OID.

Syntax

oid( variable )

Example

The following example retrieves the MDD object with local OID 10 of set mr:

select mr
from mr
where oid( mr ) = 10

The following example is incorrect as it tries to get an OID from a non-persistent result array:

select oid( mr * 2 ) -- illegal example: no expressions
from mr

Fully specified external OIDs are inserted as strings surrounded by brackets:

select mr
from mr
where oid( mr ) = < localhost | RASBASE | 10 >

In that case, the specified system (system name where the database server runs) and database must match the one used at query execution time, otherwise query execution will result in an error.

4.13.1. Expressions

Parentheses

All operators, constructors, and functions can be nested arbitrarily, provided that each sub-expression’s result type matches the required type at the position where the sub-expression occurs. This holds without limitation for all arithmetic, Boolean, and array-valued expressions. Parentheses can (and should) be used freely if a particular desired evaluation precedence is needed which does not follow the normal left-to-right precedence.

Example

select (rgb.red + rgb.green + rgb.blue) / 3c
from rgb

Operator Precedence Rules

Sometimes the evaluation sequence of expressions is ambiguous, and the different evaluation alternatives have differing results. To resolve this, a set of precedence rules is defined. You will find out that when­ever operators have their counterpart in programming languages, the rasdaman precedence rules follow the same rules as are usual there.

Here the list of operators in descending strength of binding:

• dot “.”, trimming, section
• unary -
• sqrt, sin, cos, and other unary arithmetic functions
• *, /
• +, -
• <, <=, >, >=, !=, =
• and
• or, xor
• “:” (interval constructor), condense, marray
• overlay, concat
• In all remaining cases evaluation is done left to right.

4.14. Null Values

“Null is a special marker used in Structured Query Language (SQL) to indicate that a data value does not exist in the database. NULL is also an SQL reserved keyword used to identify the Null special marker.” (Wikipedia) In fact, null introduces a three-valued logic where the result of a Boolean operation can be null itself; likewise, all other operations have to respect null appropriately. Said Wikipedia article also discusses issues the SQL language has with this three-valued logic.

For sensor data, a Boolean null indicator is not enough as null values can mean many different things, such as “no value given”, “value cannot be trusted”, or “value not known”. Therefore, rasdaman refines the SQL notion of null:

• Any value of the data type range can be chosen to act as a null value;
• a set of cell values can be declared to act as null (in contrast to SQL where only one null per attribute type is foreseen).

Caveat

Note that defining values as nulls reduces the value range available for known values. Additionally, computations can yield values inadvertently (null values themselves are not changed during operations, so there is no danger from this side). For example, if 5 is defined to mean null then addition of two non-null values, such as 2+3, yields a null.

Every bit pattern in the range of a numeric type can appear in the database, so no bit pattern is left to represent “null”. If such a thing is desired, then the database designer must provide, e.g., a separate bit map indicating the status for each cell.

To have a clear semantics, the following rule holds:

Uninitialized value handling

A cell value not yet addressed, but within the current domain of an MDD has a value of zero by definition; this extends in the obvious manner to composite cells.

Remark

Note the limitation to the current domain of an MDD. While in the case of an MDD with fixed boundaries this does not matter because always definition domain = current domain, an MDD with variable boundaries can grow and hence will have a varying current domain. Only cells inside the current domain can be addressed, be they uninitialized/null or not; addressing a cell outside the current domain will result in the corresponding exception.

Masks as alternatives to null

For example, during piecewise import of satellite images into a large map, there will be areas which are not written yet. Actually, also after completely creating the map of, say, a country there will be untouched areas, as normally no country has a rectangular shape with axis-parallel boundaries. The outside cells will be initialized to 0 which may or may not be defined as null. Another option is to define a Boolean mask array of same size as the original array where each mask value contains true for “cell valid” and false for “cell invalid. It depends on the concrete application which approach benefits best.

4.14.1. Nulls in Type Definition

Null values in rasdaman are associated with set types. This entails that all objects in one collection share the same null value set.

The rasdl grammar is extended with an optional null values clause:

typedef set < marrayName > [ null values spatialDomain ]
setName;

The set of null values syntactically is expressed as a spatialDomain element holding any number of values or intervals.

Additionally, rasql type definition allows null value definition, see Type Definition Using rasdl.

Limitation

Currently, only atomic null values can be indicated. They apply to all components of a composite cell simultaneously. In future it may become possible to indicate null values individually per struct component.

Example

The following definition establishes a null value set holding all values between 0 and 2, equal to 100, and between 250 and 255 (intervals are inclusive):

typedef set <GreyImage> null values [0:2,100,250:255]
GreySetWithNulls;

For floating-point data it is recommended to always specify small intervals instead of single numbers like 100.

Example

Set NaN values, as well as any values in the interval [-2.1e+10:-2.0e+10], as null values in the DoubleSetWithNulls set type:

typedef set <DoubleImage> null values [nan, -2.1e+10:-2.0e+10] DoubleSetWithNulls;

4.14.2. Nulls in MDD-Valued Expressions

Dynamically Set/Replace the Null Set

The null set of an MDD value resulting from a sub-expression can be dynamically changed on-the-fly with a postfix null values operator as follows:

mddExp null values nullSet

As a result mddExp will have the null values specified by nullSet; if mddExp already had a null set, it will be replaced.

Null Set Propagation

The null value set of an MDD is part of its type definition and, as such, is carried along over the MDD’s lifetime. Likewise, MDDs which are generated as intermediate results during query processing have a null value set attached. Rules for constructing the output MDD null set are as follows:

• The null value set of an MDD generated through an marray operation is empty [13].
• The null value set of an operation with one input MDD object is identical to the null set of this input MDD.
• The null value set of an operation with two input MDD objects is the union of the null sets of the input MDDs.
• The null value set of an MDD expression with a postfix null values operator is equal to the null set specified by it.

Null Values in Operations

Subsetting (trim and slice operations, as well as struct selection, etc.) perform just as without nulls and deliver the original cell values, be they null (relative to the MDD object on hand) or not. The null value set of the output MDD is the same as the null value set of the input MDD.

In MDD-generating operations with only one input MDD (such as marray and unary induced operations), if the operand of a cell operation is null then the result of this cell operation is null.

Generally, if somewhere in the input to an individual cell value com­put­at­ion a null value is encountered then the overall result will be null - in other words: if at least one of the operands of a cell operation is null then the overall result of this cell operation is null.

Exceptions:

• Comparison operators (that is: ==, !=, >, >=, <, <=) encountering a null value will always return a Boolean value; for example, both n == n and n != n (for any null value n) will evaluate to false.
• In a cast operation, nulls are treated like regular values.
• In a scale() operation, null values are treated like regular values [14].
• Format conversion of an MDD object ignores null values. Conversion from some data format into an MDD likewise imports the actual cell values; however, during any eventual further processing of the target MDD as part of an update or insert statement, cell values listed in the null value set of the pertaining MDD definition will be interpreted as null and will not overwrite persistent non-null values.

Choice of Null Value

If an operation computes a null value for some cell, then the null value effectively assigned is determined from the MDD’s type definition.

If the overall MDD whose cell is to be set has exactly one null value, then this value is taken. If there is more than one null value available in the object’s definition, then one of those null values is picked non-deterministically. If the null set of the MDD is empty then no value in the MDD is considered a null value.

Example

Assume an MDD a holding values <0, 1, 2, 3, 4, 5> and a null value set of {2, 3}. Then, a*2 might return <0, 2, 2, 2, 8, 10>. However, <0, 2, 3, 3, 8, 10> and <0, 2, 3, 2, 8, 10> also are valid results, as the null value gets picked non-deterministically.

4.14.3. Nulls in Aggregation Queries

In a condense operation, cells containing nulls do not contribute to the overall result (in plain words, nulls are ignored).

The scalar value resulting from an aggregation query does not any longer carry a null value set like MDDs do; hence, during further processing it is treated as an ordinary value, irrespective of whether it has represented a null value in the MDD acting as input to the aggregation operation.

4.14.4. Limitations

All cell components of an MDD share the same same set of nulls, it is currently not possible to assign individual nulls to cell type components.

4.14.5. NaN Values

NaN (“not a number”) is the representation of a numeric value representing an undefined or unrepresentable value, especially in floating-point calculations. Systematic use of NaNs was introduced by the IEEE 754 floating-point standard (Wikipedia).

In rasql, nan (double) and nanf (float) are symbolic floating point constants that can be used in any place where a floating point value is allowed. Arithmetic operations involving nans always result in nan. Equality and inequality involving nans work as expected, all other comparison operators return false.

If the encoding format used supports NaN then rasdaman will encode/decode NaN values properly.

Example

select count_cells( c != nan ) from c

4.15. Miscellaneous

4.15.1. rasdaman version

Builtin function version() returns a string containing information about the rasdaman version of the server, and the gcc version used for compiling it. The following query

select version()

will generate a 1-D array of cell type char containing contents similar to the following:

rasdaman 9.6.0 on x86_64-linux-gnu, compiled by g++
(Ubuntu 5.4.1-2ubuntu1~16.04) 5.4.1 20160904

Warning

The message syntax is not standardized in any way and may change in any rasdaman version without notice.

4.15.2. Retrieving Object Metadata

Sometimes it is desirable to retrieve metadata about a particular array. To this end, the dbinfo() function is provided. It returns a 1-D char array containing a JSON encoding of key array metadata:

• Object identifier;
• Base type, in rasdl notation;
• Total size of the array;
• Number of tiles and further tiling information: tiling scheme, tile size (if specified), and tile configuration;
• Index information: index type, and further details depending on the index type.

The output format is described below by way of an example.

Syntax

dbinfo( mddExp )

Example

$ rasql -q 'select dbinfo(c) from mr2 as c' --out string
{
  "oid": "150529",
  "baseType": "marray <char>",
  "tileNo": "1",
  "totalSize": "54016B",
  "tiling": {
    "tilingScheme": "no_tiling",
    "tileSize": "2097152",
    "tileConfiguration": "[0:511,0:511]"
  },
  "index": {
    "type": "rpt_index",
    "indexSize": "0",
    "PCTmax": "4096B",
    "PCTmin": "2048B"
  }
}

Note

This function can only be invoked on persistent MDD objects, not on derived (transient) MDDs.

Warning

This function is in beta. While output syntax is likely to remain largely unchanged, invocation syntax is expected to change to something like

describe array oidExp

4.16. Arithmetic Errors and Other Exception Situations

During query execution, a number of situations can arise which prohibit to deliver the desired query result or database update effect. If the server detects such a situation, query execution is aborted, and an error exception is thrown. In this Section, we classify the errors that occur and describe each class.

However, we do not go into the details of handling such an exception - this is the task of the application program, so we refer to the resp. API Guides.

4.16.1. Overflow

Candidates

Overflow conditions can occur with add_cells and induced operations such as +.

System Reaction

The overflow will be silently ignored, producing a result represented by the bit pattern pruned to the available size. This is in coherence with overflow handling in programming languages.

Remedy

Query coding should avoid potential overflow situations by applying numerical knowledge - simply said, the same care should be applied as always when dealing with numerics.

Example

Obtaining an 8-bit grey image from a 3*8-bit colour image through

( a.red + a.green + a.blue ) / 3c

most likely will result in an overflow situation after the additions, and scaling back by the division cannot remedy that. Better is to scale before adding up:

a.red / 3c + a.green / 3c + a.blue / 3c

However, this may result in accuracy loss in the last bits. So the final suggestion is to use a larger data type for the interim computation and push back the result into an 8-bit integer:

(char) ( (float)a.red+(float)a.green+(float)a.blue) / 3 )

Another option is to capture and replace overflow situations:

case
when a.red+a.green+a.blue > 255 then 255
else a.red+a.green+a.blue
end

Obviously, this will be paid with some performance penalty due to the more expensive float arithmetics. It is up to the application developer to weight and decide.

4.16.2. Illegal operands

Candidates

Division by zero, non-positive argument to logarithm, negative arguments to the square root operator, etc. are the well-known candidates for arithmetic exceptions.

The IEEE 754 standard lists, for each operation, all invalid input and the corresponding operation result (Sections Select Clause: Result Preparation, From Clause: Collection Specification, Multidimensional Intervals). Examples include:

• division(0,0), division(INF,INF)
• sqrt(x) where x < 0
• log(x) where x < 0

System Reaction

In operations returning floating point numbers, results are produced in conformance with IEEE 754. For example, 1/0 results in nan.

In operations returning integer numbers, results for illegal operations are as follows:

• div(x, 0) leads to a “division by zero” exception
• mod(x, 0) leads to a “division by zero” exception

Remedy

To avoid an exception the following code is recommended for a div b (replace accordingly for mod), replacing all illegal situations with a result of choice, c:

case when b = 0 then c else div(a, b) end

4.16.3. Access Rights Clash

If a database has been opened in read-only mode, a write operation will be refused by the server; “write operation” meaning an insert, update, or delete statement.

4.17. Database Retrieval and Manipulation

4.17.1. Collection Handling

Create a Collection

The create collection statement is used to create a new, empty MDD collection by specifying its name and type. The type must exist in the database schema. There must not be another collection in this database bearing the name indicated.

Syntax

create collection collName typeName

Example

create collection mr GreySet

Drop a Collection

A database collection can be deleted using the drop collection statement.

Syntax

drop collection collName

Example

drop collection mr1

Alter Collection

The type of a collection can be changed using the alter collection statement. The new collection type is accordingly checked for compatibility (same cell type, dimensionality) as the existing type of the collection before setting it.

Syntax

alter collection collName
set type newCollType

Example

alter collection mr2
set type GreySetWithNullValues

Retrieve All Collection Names

With the following rasql statement, a list of the names of all collections currently existing in the database is retrieved; both versions below are equivalent:

select RAS_COLLECTIONNAMES
from RAS_COLLECTIONNAMES

select r
from RAS_COLLECTIONNAMES as r

Note that the meta collection name, RAS_COLLECTIONNAMES, must be written in upper case only. No operation in the select clause is permitted. The result is a set of one-dimensional char arrays, each one holding the name of a database collection. Each such char array, i.e., string is terminated by a zero value (‘0’).

4.17.2. Select

The select statement allows for the retrieval from array collections. The result is a set (collection) of items whose structure is defined in the select clause. Result items can be arrays, atomic values, or structs. In the where clause, a condition can be expressed which acts as a filter for the result set. A single query can address several collections.

Syntax

select resultList
from collName [ as collIterator ]
     [, collName [ as collIterator ] ] ...

select resultList
from collName [ as collIterator ]
     [, collName [ as collIterator ] ] ...
where booleanExp

Examples

This query delivers a set of grayscale images:

select mr[100:150,40:80] / 2
from mr
where some_cells( mr[120:160, 55:75] > 250 )

This query, on the other hand, delivers a set of integers:

select count_cells( mr[120:160, 55:75] > 250 )
from mr

Finally, this query delivers a set of structs, each one with an integer and a 2-D array component:

select struct { max_cells( a ), a }
from mr as a

4.17.3. Insert

MDD objects can be inserted into database collections using the insert statement. The array to be inserted must conform with the collection’s type definition concerning both cell type and spatial domain. One or more variable bounds in the collection’s array type definition allow degrees of freedom for the array to be inserted. Hence, the resulting collection in this case can contain arrays with different spatial domain.

Syntax

insert into collName
values mddExp

collName specifies the name of the target set, mddExp describes the array to be inserted.

Example

Add a black image to collection mr1.

insert into mr1
values marray x in [ 0:255, 0:210 ]
values 0c

See the programming interfaces described in the rasdaman Developer’s Guides on how to ship external array data to the server using insert and update statements.

4.17.4. Update

The update statement allows to manipulate arrays of a collection. Which elements of the collection are affected can be determined with the where clause; by indicating a particular OID, single arrays can be updated.

An update can be complete in that the whole array is replaced or partial, i.e., only part of the database array is changed. Only those array cells are affected the spatial domain of the replacement expression on the right-hand side of the set clause. Pixel locations are matched pairwise according to the arrays’ spatial domains. Therefore, to appropriately position the replacement array, application of the shift() function (see Shifting a Spatial Domain) can be necessary.

As a rule, the spatial domain of the righthand side expression must be equal to or a subset of the database array’s spatial domain.

Cell values contained in the update null set will not overwrite existing cell values which are not null. The update null set is taken from the source MDD if it is not empty, otherwise it will be taken from the target MDD.

Syntax

update collName as collIterator
set    updateSpec assign mddExp

update collName as collIterator
set    updateSpec assign mddExp
where  booleanExp

where updateSpec can optionally contain a restricting minterval (see examples further below):

var
var [ mintervalExp ]

Each element of the set named collName which fulfils the selection predicate booleanEpxr gets assigned the result of mddExp. The right-hand side mddExp overwrites the corresponding area in the collection element; note that no automatic shifting takes place: the spatial domain of mddExp determines the very place where to put it.

If you want to include existing data from the database in mddExp, then this needs to be specified in an additional from clause, just like in normal select queries. The syntax in this case is

update collName as collIterator
set    updateSpec assign mddExp
from   existingCollName [ as collIterator ]
       [, existingCollName [ as collIterator ] ] ...
where  booleanExp

Example

An arrow marker is put into the image in collection mr2. The appropriate part of a is selected and added to the arrow image which, for simplicity, is assumed to have the appropriate spatial domain.

Figure 4.17 Original image of collection mr2

update mr2 as a
set a assign a[0 : 179 , 0:54] + $1/2c

The argument $1 is the arrow image (Figure 4.18) which has to be shipped to the server along with the query. It is an image showing a white arrow on a black background. For more information on the use of $ variables you may want to consult the language binding guides of the rasdaman Documentation Set.

Figure 4.18 Arrow used for updating

Looking up the mr2 collection after executing the update yields the result as shown in Figure 4.19:

Figure 4.19 Updated collection mr2

Note

The replacement expression and the MDD to be updated (i.e., left and right-hand side of the assign clause) in the above example must have the same dimensionality. Updating a (lower-dimensional) section of an MDDs can be achieved through a section operator indicating the “slice” to be modified. The following query appends one line to a fax (which is assumed to be extensible in the second dimension):

update fax as f
set f[ *:* , sdom(f)[1].hi+1 ] assign $1

The example below updates target collection mr2 with data from rgb (collection that exists already in the database):

update mr2 as a
set a assign b[ 0:150, 50:200 ].red
from rgb as b

4.17.5. Delete

Arrays are deleted from a database collection using the delete statement. The arrays to be removed from a collection can be further characterized in an optional where clause. If the condition is omitted, all elements will be deleted so that the collection will be empty afterwards.

Syntax

delete from collName [ as collIterator ]
[ where booleanExp ]

Example

delete from mr1 as a
where all_cells( a < 30 )

This will delete all “very dark” images of collection mr1 with all pixel values lower than 30.

4.18. In-Situ File Archive Storage [RE]

While rasdaman establishes efficient access structures in its databases, sometimes service providers do not want to make use of these features due to the extra disk space needed: “I cannot copy my 100 TB into a database.”

The rasdaman in-situ capability provides access to MDD tiles stored in files and directories outside DBMS control. A host of different formats can is understood by rasdaman, and virtually any given archive structure can be accommodated.

Queries on such MDD objects stored in a file system are evaluated “as is”, without importing them into a database first.

4.18.1. Accessing in-situ data

Access to in-situ file data is in no way different from database access: Any select query can be sent to the rasdaman service where the in-situ files have been registered previously. Queries can access both database and in-situ tiles.

4.18.2. Registering in-situ data

Raster data that sits in files get referenced to rasdaman without importing the actual contents, by simply registering these data to the database; only access pertinent metadata are stored in the database.

All files registered in one insert statement must be compatible with the MDD type indicated.

Any of the formats understood by GDAL can be registered, as well as NetCDF and GRIB2 data. File formats are detected automatically, therefore the query does not have any reference to the file format. Files registered within one insert statement can be of different file format.

The resulting object will have an extent given by the minimal bounding box over all files registered.

Upon registration, the following plausibility checks are performed:

• Does the file exist and is it accessible to the rasdaman server?
• Is the file type understood by rasdaman?
• Does the cell type match the definition given in the insert statement?

Syntax

insert into collName referencing ( typeName )
stringLit [ mintervalExp ],
...,
stringLit [ mintervalExp ]

where stringLit contains an absolute file path under which the file is accessible by local rasdaman server instances and mintervalExp indicates the location where these files are supposed to sit in the newly generated MDD.

Example

In the following we assume greyscale TIFF images g1.tif, g2.tif, g3.tif, and g4.tif, each of extent 100*100 and all sitting in directory /my/tiff/images/*.*. Further, we assume that the resulting object should be a square of dimensionality 200*200, with each of the tiles in a corner. The following query will generate that:

insert into GreyEx referencing (GreyImage)
    "/my/tiff/images/g1.tif" [ 0:99, 0:99 ],
    "/my/tiff/images/g2.tif" [ 100:199, 0:99 ],
    "/my/tiff/images/g3.tif" [ 0:99, 100:199 ],
    "/my/tiff/images/g4.tif" [ 100:199, 100:199 ]

The resulting object covers points from the interval [0:199, 0:199].

4.18.3. De-Registering in-situ Data

De-registering files associated with an MDD object is done through a rasql delete statement; this will remove the database MDD object and remove all knowledge about the previously registered files in the database.

Syntax is identical to the usual delete statement.

If one or more of the files registered are not present any longer at the time of the object deletion this will be ignored gracefully, without aborting query processing.

Note

In a future version, the update statement will be extended to allow selective de-registration of files registered with an object.

4.18.4. Listing in-situ Data

Listing in-situ data registered with a rasdaman service will be provided in a forthcoming version, most likely through a describe command.

4.18.5. No Updating or Deleting of in-situ Data

As rasdaman assumes read-only (“guest”) access to the in-situ archive, physical change and deletion of archive files and directories is not possible through rasdaman. See above for de-registering in-situ files.

4.18.6. Errors

Below error messages and situations are explained which can happen during registration, de-registration, and access of in-situ archive data.

“Referenced file not found.”

This error occurs when one or more of the given paths are incorrect. It is always assumed that the paths are absolute. A query which generates this message is:

insert into MyGreyImages referencing (GreyImage)
    "/example/not-existing.tif" [0:99, 0:49]

if file not-existing.tif is not existing (or not in this directory).

“Referenced path not absolute.”

This error occurs when one or more of the given paths are not absolute. A query which generates this message is:

insert into MyGreyImages referencing
 (GreyImage) "./file-without-path.tif" [0:99, 0:49]

“MDD type $token unknown.”

This error occurs when the MDD type indicated (reported in $token) does not exist. A query which generates this message is:

insert into MyGreyImages referencing (NonExistentType)
    "/example/my-file.tif" [0:99, 0:49]

if no type named NonExistentType is existing in the database.

“MDD and collection types are incompatible.”

This error occurs when the given MDD type is not compatible with the collection type. A query that generates this error is:

insert into MyGreyImages referencing (RGBImage)
    "/example/my-rgb-file.tif" [0:99, 0:49]

assuming collection MyGreyImages is of type GreySet instead of RGBImage as indicated in the query.

“Query contains overlapping tiles.”

This error occurs when two or more files passed as referencing arguments have intersecting domains. Such situations are currently not supported in rasdaman. A query which generates this error is:

insert into MyGreyImages referencing (GreyImage)
    "/examples/my-image-1.tif" [0:50, 0:49],
    "/examples/my-image-2.tif" [49:60, 0:49]

These files are indicated to have in common the sector [49:50, 0:49], hence they overlap.

De-registration errors

There are no particular error conditions which pertain to in-situ files as such.

Data access errors

When accessing a file in the course of a select query evaluation, first some plausibility checks are executed to make sure the actual file contents still conforms with rasdaman’s perception, This is necessary as the archive files are not under DBMS control, but can be modified or deleted by archive management software, human administrators, or other entities.

If rasdaman detects an inconsistency during these plausibility checks, query processing aborts with an appropriate error message.

4.19. User-Defined Functions - UDFs [RE]

4.19.1. Overview

Wikipedia teaches, “In SQL databases, User-Defined Functions (UDFs) pro­vide a mechanism for extending the functionality of the database server by adding a function that can be evaluated in SQL statements.” This mechanism is available in rasdaman enterprise, too: Functions whose implementation is provided separately, not implemented in the data­base engine, can be added at any time and then get invoked as part of expressions in rasql queries. This includes SELECT statements, where the function can be used against data stored in database collections. Con­ceptually, the function is evaluated once per collection element.

Where the SQL standard distinguishes between scalar and table funct­ions, rasql instead knows scalar and array functions. A scalar function re­turns only a single value (or NULL), whereas an array function returns a ras­daman array.

UDFs in rasdaman can be used in manifold situations. For ad-hoc functionality extension, a UDF may be defined directly in the database, including the source code implementing the function; this code will be compiled and linked on demand. Alternatively, implementation may be provided externally, as a precompiled shared library. Not only allows this to implement dedicated functionality, but it is a gateway to manifold existing tools which users may want to combine with rasdaman, such as Matlab™, R™, or ScalaPack™ (all trademarks of external tools mentioned here duly respected).

The following subsections detail invocation and man­agement of UDFs.

4.19.2. Invoking a UDF

A UDF behaves like an ordinary rasdaman function and, therefore, can be used in a straightforward way in expressions. The data type of the result is the one specified at the function creation time, so, depending on the result, a UDF expression can return either a scalar or an MDD operand.

The types of both input and output parameter expressions must match with the UDF definition, otherwise an exception is reported.

Syntax

namespace . fn ( par1, par2, ..., parn )

where

• namespace is an Identifier,
• fn is an Identifier,
• par1, …, parn are expressions acting as input parameters to f

Example

Assume a package matr for matrix operations, containing an operation transpose(mddExp) which transposes a matrix. This function can be invoked as follows:

select encode( matr.transpose( m ), "jpeg")
from MyMatrices as m

4.19.3. Creating a UDF

New functions are defined in rasdaman through the create function statement. Definition of UDFs follows standard SQL syntax.

A UDF definition is local to the particular rasdaman database where it is stored, so it is only known in this context.

Properties

A UDF is characterized by several properties.

• Namespace – establishes a grouping of functions. Namespace identifiers must be unique within a given database.

• Function name – the identifier of the function, used for invoking it in a query. Function names must be unique within a given name­space.

• Return type – the data type to be returned as the result of the function. This can be a numeric value (all rasdaman types are available, except complex and complex2 currently), string (enclosed in double quotes), or an array.

• Language – the programming language in which the UDF’s body is expressed. Currently supported:

  • cpp – this identifies GNU C++ code

• Blocking – specifies whether the function needs to see all tiles. A block­ing function will collect all tiles first so that the array passed act­u­al­ly comprises the complete object. A non-blocking function, on the other hand, will be invoked on each tile as it appears during query eval­uation.

  Generally, non-blocking operations are less main memory intensive and lend themselves better to query optimization. However, in some cases (e.g., when a function needs to see the array as a whole for its an­alysis) a function needs to be declared as blocking.

  Default: blocking.

• Determinism - specifies whether the function is deterministic or not. A de­terministic function will deliver the same result when invoked with the same parameters, whereas a nondeterministic function may deliver results that vary from call to call. This property has influence on the query optimizer: deterministic functions can be considered by Common Subexpression Elimination.

  Default: deterministic.

• Code block – the implementation of the function.

Syntax

create function namespace . fn
( typeName1 var1, ..., typeNameN varN )
returns typeName
language lang
[ blocking | nonblocking ]
[ deterministic | nondeterministic ]
code

where

• namespace is an Identifier,
• fn is an Identifier,
• typeName…, typeNameN are Identifiers
• var1, …, varN are Identifiers
• lang is cpp,
• code is explained below.

Code body provision

The code implementing the UDF can be provided in two ways: ad-hoc or as an external file. In both variants, the code provided will be compiled and linked into the server engine at runtime.

In the ad-hoc case, the function body is provided as program text enclosed in begin and end keywords:

begin
code block
end

Alternatively, the code implementing the function can be stored in an external file; in this case, the path leading to the file is specified relative to the UDF directory:

extern "/path/filename"

The target file must exist and be readable by rasserver. If rasdaman cannot access the object code file it will abort query execution with a UDF exception.

For security reasons it is strongly advisable to restrict access to the UDFs so that no unauthorized code modification can be performed.

Parameter types

UDFs can receive and return any rasql atomic type, plus strings, plus arrays; the same type identifiers are used as in rasdl:

• octet - signed 1 byte integer type
• char - unsigned 1 byte integer type
• short - signed 2 bytes integer type
• ushort - unsigned 2 bytes integer type
• long - signed 4 bytes integer type
• ulong - unsigned 4 bytes integer type
• float - 4 bytes single precision floating point type
• double - 8 bytes double precision floating point type
• bool - 1 bit true/false type
• string - sequence of characters, enclosed in double quotes
• array - multidimensional type; note that neither cell type nor extent are indicated, detailed type information is passed dynamically through the C++ API.

Examples

In the first example, the function fib() produces Fibonacci numbers. The source code is provided verbatim as function body (note that no function header is provided in the code block):

create function math.fib ( long n ) returns long
language cpp deterministic
begin
if (n == 0 || n == 1) {
  return n;
} else {
  return fib(n - 1) + fib(n - 2);
}
end

In the second example, non-blocking function avg() belonging to namespace stat receives an array and delivers an unsigned short result. The compiled code is provided by the administrator in UDF subdirectory stat/ as file average.so, and needs to be referenced accordingly:

create function stat.avg( array a ) returns ushort
language cpp nonblocking
extern "stat/average.so"

See the next section for the placement of UDF code and following section for guidance on writing external UDF code.

4.19.4. Code location

UDF code is stored in subdirectory $RMANHOME/share/rasdaman/udf/.

UDF organization

Having many UDFs in the same directory (potentially even with their source code and related files) may make administration unwieldy. Therefore, the udf/ directory can contain any number of subdirectories, with arbitrary naming and depth. Note that such subpaths must be indicated correctly in the create function statement, such as

extern "math/average.so"

For UDF subpaths a convention is used by rasdaman, and it is re­comm­end­ed to follow it for externally provided code, too.

Ad-hoc provided code is compiled by rasdaman into a subdirectory udf/ named after its namespace:

/opt/rasdaman/share/rasdaman/udf/ns/

whereby ns is the identifier of the namespace to which the UDF code belongs.

Note that in such a folder intermediary files may be generated by ras­da­man when compiling the UDF. All those files – including those possibly located by the administrator, such as source code, Makefiles, docu­ment­ation, etc. – are ignored by rasdaman.

Placement of working directories

Upon installation, the directory is placed in the rasdaman directory tree. Typically, it will not occupy much space and there is only very moderate change applied (upon addition or deletion of new types as well as upon compilation of a UDF), so neither disk space nor access frequency should have noticeable impact on the system.

Still, it is always an option for the administrator, of course, to symlink this directory into some other location, such as /var/lib/rasdaman/udf.

4.19.5. Writing UDF Code

Any C or C++ code can be linked into rasdaman as a UDF, provided a few conventions are followed:

• The external source file must define a function with the same name as the function defined in the UDF from the rasdaman viewpoint.
• In a C++ environment, this function must be declared extern "C" to avoid name mangling.
• Function input parameters as well as result must match with the corresponding UDF definition.

Parameter passing

Parameter passing between the rasdaman engine and UDFs is made as convenient as possible through intelligent transparent conversion:

• Numerical values are passed directly. Equivalence between rasql and pro­gramming language data type is straightforward as suggested by the type names.

• Strings are passed as char* pointers.

• Arrays are passed into UDFs and accepted from UDFs as objects of class r_GMarray. This class is defined in the rasdaman header file rasodmg/gmarray.hh which the UDF code must include (see the raslib and rasodmg C++ API documentation).

  Note that this mechanism is used for both complete arrays (in case of a blocking function) and for single tiles (in case of a nonblocking function). In other words, tiles are converted to r_GMArray before rasdaman passes them to a UDF, and arrays returned to rasdaman are converted from r_GMArray into tiles where necessary.

Error handling

Abnormal return are reported according to regular programming language conventions:

• Following standard conventions, numeric data types do not have any reserved value, so they cannot report back error conditions. In other words, rasdaman will accept any value passed back as valid result.
• A null pointer passed back (in case of return type string or array) will be interpreted as an error and raise a UDF exception in rasdaman, which will then be reported back to the client which has submitted the overall query.
• An exception thrown during UDF execution will be mapped to a rasdaman UDF exception, which will then be reported back to the client which has submitted the overall query.

Example

Assume the above example function fib() is now implemented as an external function, to be compiled by the user. The corresponding source code may look as follows:

extern "C" long fib(long n)
{
  if (n == 0 || n == 1)
    return n;
  else
    return fib(n - 1) + fib(n - 2);
}

This source can be compiled into a shared library using

g++ -O2 -fPIC -shared -Wl,-soname,myfib.so -o myfib.so myfib.cpp

The dynamic library file, myfib.so, must be placed in the UDF directory for use by rasdaman. If it is to become part of namespace math/ it should be placed into UDF directory math/myfib.so.

4.19.6. Deleting a UDF

A UDF can be deleted from the database if it is not needed anymore. This operation requires the right to modify the database.

Syntax

delete function namespace . fn

Example

delete function math.fib

4.19.7. Listing all UDFs

A list of all UDFs currently registered in the database can be obtained using rasql. The result of this query is a list of 1-D char arrays containing the namespace and the name of the functions in the current instance of the rasdaman database.

Syntax

select view function list

Example

$ rasql --out string -q "select view function list"
opening database RASBASE at localhost:7001...ok
Executing retrieval query...ok
Query result collection has 1 element(s):
Result object 1: Registered functions:
testfunctions.f1
testfunctions.f2
rasql done.

4.19.8. Retrieving a UDF body

The definition of a UDF, i.e., its function header and body, can be retrieved via rasql as well. The result of this query is the function declaration as provided at creation time.

Syntax

select get function namespace . fn

Example

$ rasql --out string -q "select get function testfunctions.f1"
opening database RASBASE at localhost:7001...ok
Executing retrieval query...ok
Query result collection has 1 element(s):
Result object 1: create function testfunctions.f1
long a, double b, char c
returns double
language cpp
not blocking
deterministic
begin
return b;
end
rasql done.

4.20. Transaction Scheduling

Since rasdaman 9.0, database transactions lock arrays on fine-grain level. This prevents clients from changing array areas currently being modified by another client.

4.20.1. Locking

Lock compatibility is as expected: read access involves shared (“S”) locks which are mutually compatible while write access imposes an exclusive lock (“X”) which prohibits any other access:

	S	X
S	+	-
X	-	-

Shared locks are set by SELECT queries, exclusive ones in INSERT, UPDATE, and DELETE queries.

Locks are acquired by queries dynamically as needed during a trans­action. All locks are held until the end of the transaction, and then released collectively [15].

4.20.2. Lock Granularity

The unit of locking is a tile, as tiles also form the unit of access to persistent storage.

4.20.3. Conflict Behavior

If a transaction attempts to acquire a lock on a tile which has an incompatible lock it will abort with a message similar to the following:

Error: One or more of the target tiles are locked by another
transaction.

Only the query will return with an exception, the rasdaman transaction as such is not affected. It is up to the application program to catch the exception and react properly, depending on the particular intended behaviour.

4.20.4. Lock Federation

Locks are maintained in the PostgreSQL database in which rasdaman stores data. Therefore, all rasserver processes accessing the same RASBASE get synchronized.

4.20.5. Examples

The following two SELECT queries can be run concurrently against the same database:

rasql -q "select mr[0:10,0:10] from mr"

rasql -q "select mr[5:10,5:10] from mr"

The following two UPDATE queries can run concurrently as well, as they address different collections:

rasql -q "update mr set mr[0:10,0:10] \
          assign marray x in [0:10,0:10] values 127c" \
      --user rasadmin --passwd rasadmin

rasql -q "update mr2 set mr2[0:5,0:5] \
          assign marray x in [0:5,0:5] values 65c" \
      --user rasadmin --passwd rasadmin

From the following two queries, one will fail (the one which happens to arrive later) because the address the same tile:

rasql -q "update mr set mr[0:10,0:10] assign \
          marray x in [0:10,0:10] values 127c" \
      --user rasadmin --passwd rasadmin

rasql -q "update mr set mr[0:5,0:5] assign \
          marray x in [0:5,0:5] values 65c" \
      --user rasadmin --passwd rasadmin

4.20.6. Limitations

Currently, only tiles are locked, not other entities like indexes.

4.21. Linking MDD with Other Data

4.21.1. Purpose of OIDs

Each array instance and each collection in a rasdaman database has a identifier which is unique within a database. In the case of a collection this is the collection name and an object identifier (OID), whereas for an array this is only the OID. OIDs are generated by the system upon creation of an array instance, they do not change over an array’s lifetime, and OIDs of deleted arrays will never be reassigned to other arrays. This way, OIDs form the means to unambiguously identifiy a particular array. OIDs can be used several ways:

• In rasql, OIDs of arrays can be retrieved and displayed, and they can be used as selection conditions in the condition part.
• OIDs form the means to establish references from objects or tuples residing in other databases systems to rasdaman arrays. Please refer for further information to the language-specific rasdaman Developer’s Guides and the rasdaman External Products Integration Guide available for each database system to which rasdaman interfaces.

Due to the very different referencing mechanisms used in current database technology, there cannot be one single mechanism. Instead, rasdaman employs its own identification scheme which, then, is combined with the target DBMS way of referencing. See Object identifier (OID) Constants of this document as well as the rasdaman External Products Integration Guide for further information.

4.21.2. Collection Names

MDD collections are named. The name is indicated by the user or the application program upon creation of the collection; it must be unique within the given database. The most typical usage forms of collection names are

• as a reference in the from clause of a rasql query
• their storage in an attribute of a base DBMS object or tuple, thereby establishing a reference (also called foreign key or pointer).

4.21.3. Array Object identifiers

Each MDD array is world-wide uniquely identified by its object identifier (OID). An OID consists of three components:

• A string containing the system where the database resides (system name),
• A string containing the database (base name), and
• A number containing the local object id within the database.

The main purposes of OIDs are

• to establish references from the outside world to arrays and
• to identify a particular array by indicating one OID or an OID list in the search condition of a query.

4.22. Storage Layout Language

4.22.1. Overview

Tiling

To handle arbitrarily large arrays, rasdaman introduces the concept of tiling them, that is: partitioning a large array into smaller, non-overlapping sub-arrays which act as the unit of storage access during query eval­uat­ion. To the query client, tiling remains invisible, hence it constitutes a tun­ing parameter which allows database designers and administrators to adapt database storage layout to specific query patterns and workloads.

To this end, rasdaman offers a storage layout language for arrays which embeds into the query language and gives users comfortable, yet concise control over important physical tuning parameters. Further, this sub-language wraps several strategies which turn out useful in face of massive spatio-temporal data sets.

Tiling can be categorized into aligned and non-aligned (Figure 4.20).A tiling is aligned if tiles are defined through axis-parallel hyperplanes cutting all through the domain. Aligned tiling is further classified into regular and aligned irregular depending on whether the parallel hyperplanes are equidistant (except possibly for border tiles) or not. The special case of equally sized tile edges in all directions is called cubed.

Figure 4.20 Types of tilings

Non-aligned tiling contains tiles whose faces are not aligned with those of their neighbors. This can be partially aligned with still some hyperplanes shared or totally non-aligned with no such sharing at all.

Syntax

We use a BNF variant where optional elements are indicated as

( ... )?

to clearly distinguish them from the “[” and “]” terminals.

Tiling Through API

In the rasdaman C++ API (cf. C++ Guide), this functionality is available through a specific hierarchy of classes.

Introductory Example

The following example illustrates the overall syntax extension which the storage layout sublanguage adds to the insert statement:

insert into MyCollection
values ...
tiling
    area of interest [0:20,0:40],[45:80,80:85]
    tile size 1000000

4.22.2. General Tiling Parameters

Maximum Tile Size

The optional tile size parameter allows specifying a maximum tile size; irrespective of the algorithm employed to obtain a particular tile shape, its size will never exceed the maximum indicated in this parameter.

Syntax:

tile size t

where t indicates the tile size in bytes.

If nothing is known about the access patterns, tile size allows stream­lining array tiling to architectural parameters of the server, such as DMA bandwidth and disk speed.

Tile Configuration

A tile configuration is a list of bounding boxes specified by their extent. No position is indicated, as it is the shape of the box which will be used to define the tiling, according to various strategies.

Syntax:

[ integerLit , ... , integerLit ]

For a d-dimensional MDD, the tile configuration consists of a vector of d elements where the i^th vector specifies the tile extent in dimension i, for 0lei<d. Each number indicates the tile extent in cells along the corresp­ond­ing dimension.

For example, a tile configuration [100, 100, 1000] for a 3-D MDD states that tiles should have an extent of 100 cells in dimension 0 and 1, and an extent of 1,000 cells in dimension 2. In image timeseries analysis, such a stretching tiles along the time axis speeds up temporal analysis.

4.22.3. Regular Tiling

Concept

Regular tiling applies when there is some varying degree of knowledge about the subsetting patterns arriving with queries. We may or may not know the lower corner of the request box, the size of the box, or the shape (i.e., edge size ratio) of the box. For example, map viewing clients typically send several requests of fixed extent per mouse click to maintain a cache of tiles in the browser for faster panning. So the extent of the tile is known – or at least that tiles are quadratic. The absolute location often is not known, unless the client is kind enough to always request areas only in one fixed tile size and with starting points in multiples of the tile edge length.If additionally the configuration follows a uniform probability distrib­ut­ion then a cubed tiling is optimal.

In the storage directive, regular tiling is specified by providing a bounding box list, TileConf, and an optional maximum tile size:

Syntax

tiling regular TileConf ( tile size integerLit )?

Example

This line below dictates, for a 2-D MDD, tiles to be of size 1024 x 1024, except for border tiles (which can be smaller):

tiling regular [ 1024 , 1024 ]

4.22.4. Aligned Tiling

Concept

Generalizing from regular tiling, we may not know a good tile shape for all dimensions, but only some of them. An axis pin { 1, …, d } which never participates in any subsetting box is called a preferred (or pre­fer­ential) direction of access and denoted as tc_p = *. An optimal tile structure in this situation extends to the array bounds in the preferential directions.

Practical use cases include satellite image time series stacks over some reg­ion. Grossly simplified, during analysis there are two distinguished acc­ess patterns (notwithstanding that others occur sometimes as well): either a time slice is read, corresponding to tc = (*, *, t) for some given time instance t, or a time series is extracted for one particular position (x, y) on the earth surface; this corresponds to tc = ( x, y, *). The aligned tiling alg­or­ithm creates tiles as large as possible based on the constraints that (i) tile pro­portions adhere to tc and (ii) all tiles have the same size. The upper array limits constitute an exception: for filling the remaining gap (which us­ually occurs) tiles can be smaller and deviate from the con­fig­ur­ation siz­ings. Figure 4.21 illustrates aligned tiling with two examples, for configuration tc = (1, 2) (left) and for tc =(1, 3, 4) (right).

Figure 4.21 Aligned tiling examples

Preferential access is illustrated in Figure 4.22. Left, access is performed along preferential directions 1 and 2, corresponding to configuration tc = (*, *, 1). The tiling tothe right supports configuration tc = (4, 1, *) with preferred axis 3.

Figure 4.22 Aligned tiling examples with preferential access directions

The aligned tiling construction consists of two steps. First, a concrete tile shape is determined. After that, the extent of all tiles is calculated by iterating over the array’s complete domain. In presence of more than one preferred directions - i.e., with a configuration containing more than one “*” values - axes are prioritized in descending order. This exploits the fact that array linearization is performed in a way that the “outermost loop” is the first dimension and the “innermost loop” the last. Hence, by clustering along higher coordinate axes a better spatial clustering is achieved.

Syntax

tiling aligned TileConf ( tile size IntLit )?

Example

The following clause accommodates map clients fetching quadratic images known to be no more than 512 x 512 x 3 = 786,432 bytes:

tiling aligned [1,1] tile size 786432

Important

Aligned tiling is the default strategy in rasdaman.

4.22.5. Directional Tiling

Concept

Sometimes the application semantics prescribes access in well-known coordinate intervals. In OLAP, such intervals are given by the semantic categories of the measures as defined by the dimension hierarchies, such as product categories which are defined for the exact purpose of accessing them group-wise in queries. Similar effects can occur with spatio-temporal data where, for example, a time axis may suggest access in units of days, weeks, or years. In rasdaman, if bounding boxes are well known then spatial access may be approximated by those; if they are overlapping then this is a case for area-of-interest tiling (see below), if not then directional tiling can be applied.

The tiling corresponding to such a partition is given by its Cartesian product. Figure 4.23 shows such a structure for the 2-D and 3-D case.

To construct it, the partition vectors are used to span the Cartesian product first. Should one of the resulting tiles exceed the size limit, as it happens in the tiles marked with a “*” in Figure 4.23, then a so-called sub-tiling takes place. Sub-tiling applies regular tiling by introducing additional local cutting hyperplanes. As these hyperplanes do not stretch through all tiles the resulting tiling in general is not regular. The resulting tile set guarantees that for answering queries using one of the subsetting patterns in part, or any union of these patterns, only those cells are read which will be delivered in the response. Further, if the area requested is smaller than the tile size limit then only one tile needs to be accessed.

Figure 4.23 Directional tiling

Sometimes axes do not have categories associated. One possible reason is that subsetting is never performed along this axis, for example in an image time series where slicing is done along the time axis while the x/y image planes always are read in total. Similarly, for importing 4-D climate data into a GIS a query might always slice at the lowest atmospheric layer and at the most current time available without additional trimming in the horizontal axes.

We call such axes preferred access directions in the context of a directional tiling; they are identified by empty partitions. To accommodate this intention expressed by the user the sub-tiling strategy changes: no longer is regular tiling applied, which would introduce undesirable cuts along the preferred axis, but rather are subdividing hyperplanes constructed parallel to the preference axis. This allows accommodating the tile size maximum while, at the same time, keeping the number of tiles accessed in preference direction at a minimum.

In Figure 4.24, a 3-D cube is first split by way of directional tiling (left). One tile is larger than the maximum allowed, hence sub-tiling starts (center). It recognizes that axes 0 and 2 are preferred and, hence, splits only along dimension 1. The result (right) is such that subsetting along the preferred axes - i.e., with a trim or slice specification only in dimension 1 - can always be accommodated with a single tile read.

Figure 4.24 Directional tiling of a 3-D cube with one degree of freedom

Syntax

tiling directional splitList
( with subtiling ( tile size integerLit)? )?

where splitList is a list of split vectors (t_1,1; …; t_1,n1),…,(t_d,1; …; t_d,nd). Each split vector consists of an ascendingly ordered list of split points for the tiling algorithm, or an asterisk “*” for a preferred axis. The split vectors are positional, applying to the dimension axes of the array in order of appearance.

Example

The following defines a directional tiling with split vectors (0; 512; 1024) and (0; 15; 200) for axes 0 and 2, respectively, with dimension 1 as a pre­ferred axis:

tiling directional [0,512,1024], [], [0,15,200]

4.22.6. Area of Interest Tiling

Concept

An area of interest is a frequently accessed sub-array of an array object. An area-of-interest pattern, consequently, consists of a set of domains accessed with an access probability significantly higher than that of all other possible patterns. Goal is to achieve a tiling which optimizes access to these preferred patterns; performance of all other patterns is ignored.

These areas of interest do not have to fully cover the array, and the may overlap. The system will establish an optimal disjoint partitioning for the given boxes in a way that the amount of data and the number of tiles accessed for retrieval of any area of interest are minimized. More exactly, it is guaranteed that accessing an area of interest only reads data be­long­ing to this area.

Figure 4.25 gives an intuition of how the algorithm works. Given some area-of-interest set (a), the algorithm first partitions using directional tiling based on the partition boundaries (b). By construction, each of the resulting tiles (c) contains only cells which all share the same areas of interest, or none at all. As this introduces fragmentation, a merge step follows where adjacent partitions overlapping with the same areas of interest are combined. Often there is more than one choice to perform merging; the algorithm is inherently nondeterministic. Rasdaman exploits this degree of freedom and cluster tiles in sequence of dimensions, as this represents the sequentialization pattern on disk and, hence, is the best choice for maintaining spatial clustering on disk (d,e). In a final step, sub-tiling is performed on the partitions as necessary, depending on the tile size limit. In contrast to the directional tiling algorithm, an aligned tiling strategy is pursued here making use of the tile configuration argument, tc. As this does not change anything in our example, the final result (f) is unchanged over (e).

Figure 4.25 Steps in performing area of interest tiling**

Syntax

tiling area of interest tileConf ( tile size integerLit )?

Example

tiling area of interest
[0:20,0:40],[945:980,980:985],[10:1000,10:1000]

4.22.7. Tiling statistic

Concept

Area of interest tiling requires enumeration of a set of clearly delineated areas. Sometimes, however, retrieval does not follow such a focused pattern set, but rather shows some random behavior oscillating around hot spots. This can occur, for example, when using a pointing device in a Web GIS: while many users possibly want to see some “hot” area, coordinates sub­mitted will differ to some extent. We call such a pattern multiple acc­ess­es to areas of interest. Area of interest tiling can lead to significant dis­advantages in such a situation. If the actual request box is contained in some area of interest then the corresponding tiles will have to be pruned from pixels outside the request box; this requires a selective copying which is significantly slower than a simple memcpy(). More important, how­ever, is a request box going slightly over the boundaries of the area of int­erest - in this case, an additional tile has to be read from which only a small portion will be actually used. Disastrous, finally, is the output of the area-of-interest tiling, as an immense number of tiny tiles will be gen­er­at­ed for all the slight area variations, leading to costly merging during requ­ests.

This motivates a tiling strategy which accounts for statistically blurred access patterns. The statistic tiling algorithm re­ceiv­es a list of access patterns plus border and frequency thresholds. The algorithm condenses this list into a smallish set of patterns by group­ing them according to sim­il­ar­ity. This process is guarded by the two thresh­olds. The border thresh­old determines from what maximum diff­er­ence on two areas are considered separately. It is measured in number of cells to make it indep­end­ent from area geometry. The result is a reduced set of areas, each ass­ociated with a frequency of occurrence. In a second run, those areas are filtered out which fall below the frequency threshold. Having calculated such re­pres­ent­ative areas, the algorithm performs an area of interest tiling on these.

This method has the potential of reducing overall access costs provided thresholds are placed wisely. Log analysis tools can provide estimates for guidance. In the storage directive, statistical tiling receives a list of areas plus, optionally, the two thresholds and a tile size limit.

Syntax

tiling statistic tileConf
( tile size integerLit )?
( border threshold integerLit)?
( interest threshold floatLit)?

Example

The following example specifies two areas, a border threshold of 50 and an interest probability threshold of 30%:

tiling statistic [0:20,0:40],[30:50,70:90]
border threshold 50
interest threshold 0.3

4.22.8. Summary: Tiling Guidelines

This section summarizes rules of thumb for a good tiling. However, a thorough evaluation of the query access pattern, either empirically through server log inspection or theoretically by considering application logics, is strongly recommended, as it typically offers a potential for substantial improvements over the standard heuristics.

• Nothing is known about access patterns: choose regular tiling with a maximum tile size; on PC-type architectures, tile sizes of about 4-5 MB have yielded good results.
• Trim intervals in direction x are n times more frequent than in direction y and z together: choose directional tiling where the ratios are approximately x*n=y*z. Specify a maximum tile size.
• Hot spots (i.e., their bounding boxes) are known: choose Area of Interest tiling on these bounding boxes.

4.23. Storage Encoding and Compression [RE]

4.23.1. Specifying Storage Encoding and Compression

Concept

Storage of arrays in rasdaman is done by partitioning them into tiles, as described already in Storage Layout Language. Each tile is stored as an independent unit. By default, the storage format of tiles is the rasdaman- internal binary format. This is the only format available in rasdaman community; in rasdaman enterprise it is possible to compress tiles or select different storage formats.

Syntax

insert into collName values ...
[ storage encodingFormat [ compression compressionFormat ] ]

where

encodingFormat :
  array
| tiff
| hdf
| netcdf
| jpeg
| csv
| png

compressionFormat :
  AutoCompression
| ZLib
| SepZLib
| RLE
| SepRLE
| PACKBITS
| TMC
| HaarWavelet
| QHaarWavelet
| DaubechiesWavelet
| Daubechies6Wavelet
| Daubechies8Wavelet
| Daubechies10Wavelet
| Daubechies12Wavelet
| Daubechies14Wavelet
| Daubechies16Wavelet
| Daubechies18Wavelet
| Daubechies20Wavelet
| LeastAsym8Wavelet
| LeastAsym10Wavelet
| LeastAsym12Wavelet
| LeastAsym14Wavelet
| LeastAsym16Wavelet
| LeastAsym18Wavelet
| LeastAsym20Wavelet
| Coiflet6Wavelet
| Coiflet12Wavelet
| Coiflet18Wavelet
| Coiflet24Wavelet
| Coiflet30Wavelet
| Coiflet12Wavelet

By default, encodingFormat is array, i.e. raw byte storage. The compression subclause is only applicable on array storage encoding format, e.g. data cannot be encoded in a format like png and then further compressed.

The available compression formats are explained in full detail in the accompanying compression-guide.pdf.

Note

It is not recommended to use any other format than compressed or un­comp­ressed array. Typically, their decoding overhead is prohibitive with little gain in compression (if at all).

Example

The following query ensures that the inserted array object is stored in tiff format:

insert into mr values $1
storage tiff

We can store a binary mask compressed with RLE for example with the following query:

insert into RiverMasks values $1
storage array compression RLE

4.23.2. Errors

Below error messages and situations are explained which can happen when explicitly specifying storage format encoding or compression.

“Error in compression engine.”

This error indicates a general error with the selected compression scheme. The server logs can be further indicative about the specific error condition.

“Base type not supported by conversion/compression module.”

The selected format encoding or compression scheme does not support encoding or compressing data of this type.

“Invalid storage format specified, compression only applicable on array format.”

This error will occur when compression is attempted on encoded data, e.g:

insert into RiverMasks values $1
storage png compression ZLib

“Unsupported compression format.”

The specified compression format is invalid, e.g:

insert into RiverMasks values $1
storage array compression ZLibInvalid

“Unsupported encoding format.”

The specified encoding format is invalid, e.g:

insert into RiverMasks values $1
storage hdf5

4.24. Compression in Depth [RE]

4.24.1. Introduction

rasdaman contains a compression engine for generic multidimensional arrays (MDD), suitable for storage- and transfer compression. The goal of data compression is to transform the data into a more compact but equivalent representation, e.g. using fewer bits to represent frequent symbols and more bits to represent rarely occurring ones. The advantages of using compression are a reduction in storage space and transfer times due to the reduced data volume; the disadvantage is that compression can be very demanding on processing power.

This guide will give a short overview of compression basics and terminology in Compression Basics, continues with the compression engine’s basic architecture Compression Engine Architecture, followed by a description of the various compression algorithms and their parameters in Compression Algorithms. Next up are several examples in Examples, followed by some general hints on the use of compression in rasdaman in Hints & Tips. It closes with a detailed description of the test bed and how to use it in particular for rate-distortion analysis in Using the Compression Test Bed.

4.24.2. Compression Basics

This section introduces some important principles of data compression. If you’re familiar with compression techniques and terminology you may skip this section and continue right away with the compression engine architecture in Compression Engine Architecture.

Entropy and Compression

Assuming there are no dependencies within the data being compressed, there is a hard limit on the minimum size this data can be compressed to. The theoretical foundation for this was laid by Shannon in 1948 who defined the entropy \(H\) of symbols over an alphabet \({\mathcal A} = \{ X_1,\ldots,X_N \}\) as

(4.1)\[H(A) = - \sum\limits_{i=1}^N p(X_i)\log p(X_i)\]

where \(p(X_i)\) is the probability of symbol \(X_i\). \(H(A)\) describes the average size of a symbol in a sequence over \({\mathcal A}\); the unit depends on the base of the logarithm in (4.1) which is typically 2 and makes \(H(A)\) the average number of bits per symbol. Compression algorithms using this probabilistic model to minimize the total size are called entropy coders. The two most commonly used entropy coders today are Huffmann coding and the more advanced Arithmetic coding used in this engine.

Breaking the Entropy Boundary

Normally, there are dependencies in the symbols being processed, however. For example letters in a book are highly correlated, so the probability of an ’h’ following a ’c’ is considerably higher than that of an ’x’. That means that e.g. text can be compressed far more efficiently if the dependencies are removed before applying the entropy coder. In other words, the data is transformed (\(\rightarrow\) decorrelated) into a different representation assuming a data model (e.g. ”english text”); if the data model matches the data, the resulting representation has smaller entropy than the original one and therefore allows more efficient compression. The best results are usually achieved for alphabets with a highly skewed probability distribution where the data is concentrated around a very small number of symbols and most other symbols are highly improbable. The worst case for an entropy coder is an alphabet where every symbol has the same probability, as it can’t compress sequences over such an alphabet at all.

This principle is the basis of most modern compression designs, such as the standard compression library ZLib, the well-known JPEG image compression system and many more. It results in a two-layer architecture with a model layer on top performing the (inverse) decorrelation transformation according to a data model and a compression layer (de)compressing the transformed data.

The entropy can be reduced even further by abandoning the equivalence postulate and allowing loss of information during compression. This typically means that detail information (such as the least significant bits in an image) may be modified by the compression algorithm in such a way that the resulting data compresses better. Whether loss is acceptable and which parts of the data correspond to expendable detail information is highly application-specific, however.

Compression Terminology

There is special terminology used in the compression field to describe properties of compression algorithms; those relevant for the remainder of this document will be introduced in this section.

The compression rate is defined as the average number of bits per cell, so a compression algorithm that achieves a rate of 2 for an 8 bit cell compresses the data to 25% its raw size. In lossy compression, the rate is no longer limited by the entropy (see Entropy and Compression) but can be almost arbitrarily small – at the expense of quality, of course. An ideal compression algorithm has minimum rate and minimum loss (= distortion), but unfortunately the minimization of rate and distortion is mutually exclusive. The study of the correlations between rate and distortion is commonly known as rate-distortion theory.

Lossless compression algorithms represent the extreme case of minimum (= 0) distortion at the expense of high rate. In lossy compression, the user can specify a tradeoff between rate and distortion, e.g. achieve very low rates at the expense of quality or vice versa. Therefore an objective measure for the distortion is required in order to evaluate the performance of a lossy compression algorithm. The most commonly used approaches to compare how well a signal \(x\) (consisting of \(n\) samples \(x_1,\ldots,x_n\)) is approximated by a signal \(\hat x\) (also consisting of \(n\) samples \(\hat x_1,\ldots,\hat x_n\)) are the signal-to-noise ratio (\(SNR\)), the peak-signal-to-noise ratio (\(PSNR\)) and the residual (\(Res\)) defined as follows:

\[\begin{split}\begin{aligned} Snr& = & \frac{\sum\limits_{i=1}^n x_i^2}{\sum\limits_{i=1}^n (x_i - \hat x_i)^2} \\ Psnr& = & \frac{n \max\limits_{i=1,\ldots,n} x_i^2}{\sum\limits_{i=1}^n (x_i - \hat x_i)^2} \\ Res& = & \max\limits_{i=1,\ldots,n} |x_i - \hat x_i|. \end{aligned}\end{split}\]

\(Snr\) sets the sum of squared sample values (the signal’s energy) in relation to the squared deviation of the approximating signal from the actual one (the error’s energy), \(Psnr\) does the same with the signal’s peak energy. In case there is no error, both \(Snr\) and \(Psnr\) are \(\infty\) and \(Res\) is zero. The differences between these three approaches are in plain english:

SNR

corresponds to the inverse of the average distortion per cell

PSNR

corresponds to relative amplitude of noise floor

RES

corresponds to maximum distortion per cell

4.24.3. Compression Engine Architecture

As mentioned in Breaking the Entropy Boundary, most modern compression systems have a two-layer architecture consisting of a model layer and a compression layer. The data model in this engine is that of MDD, i.e. generic multidimensional arrays. By using the semantics of the data stored in MDD format rather than just entropy-coding the MDD’s raster data in some linearization order directly, considerably better compression rates can be achieved. Independently from its actual contents, any MDD has two properties attractive for the model layer:

1. Base Type: if the base type is structured rather than atomic, it is often more efficient to compress the channels separately rather than the interleaved default. A channel contains all cell values belonging to the same atomic type within a structured type; for instance a colour image (RGB) has three channels, one for each colour.
2. Spatial neighbourhoods: many objects modelled as MDD have a spatial interpretation (raster images, volume tomograms, spatio-temporal simulations, \(\ldots\)). Cell values in neighbouring cells are often similar (i.e. correlated) and rarely change rapidly. The way the multidimensional data is linearized within the MDD, spatial neighbourhoods are only visible in one dimension, often leading to suboptimal performance.

It is important to stress the fact that the model layer consists of heuristics and therefore can not guarantee that data compresses better the more heuristics are used. There are MDD over structured base types which compress better if the channels are interleaved, same as there are some MDD where resolving spatial correlations does not improve – or even deteriorate – compression. It is therefore impossible to suggest any compression technique as optimal, since finding the optimum usually requires experimentation. More on this will follow in Hints & Tips.

Compression granularity is also an important issue. Typically a compression algorithm performs better the more data it has to compress; this is because

• the relative size of meta data in headers (necessary for correctly decompressing the data) becomes smaller the more data is processed;
• many compression techniques are adaptive, i.e. they learn the data properties as they compress the data; that means they have to process a significant amount of data before they are able to compress it efficiently.

On the other hand, the more data is compressed in one unit, the more data needs to be decompressed if any cell within that unit is accessed, so compressing a large MDD as one unit means that accessing any cell within that MDD triggers a decompression of the entire MDD, which will cause the system to grind to a halt. rasdaman already introduced tiles for reduced access granularity, so the natural choice was to make compression operate on tile level as well. Bear in mind that therefore the tile size also represents the compression granularity and keep the tile size reasonably small if access time is more important than storage savings. The default tile size of 32kB is in many cases a good compromise and smaller tiles are discouraged if they are going to be compressed. In some cases considerably larger tiles can also be feasible, however, in particular wavelet compression of MDD with more than two dimensions. Also note that the compression technique can change between tiles of the same MDD, so it is possible to compress some tiles and keep the others uncompressed.

Compression algorithms often require parameters to function efficiently. For instance ZLib compression allows the user to choose a tradeoff between compression time and storage savings via a compression level parameter between 0 (just store) and 9 (best compression at the expense of speed). The kind and number of parameters can differ considerably between compression algorithms, therefore a very general system is needed for the compression parameters. The rasdaman compression engine supports a dynamic parameter system where the parameters are coded as strings. A parameter string consists of comma-separated pairs of keyword=value, where keyword identifies the parameter and value is the parameter value in string representation. The interpretation of the value depends on the type of the parameter; currently three parameter types are supported:

integers:

32 bit signed integer numbers

double:

double precision floating point numbers

strings:

arbitrary-length strings. If the string contains either whitespace characters or commas, it must be enclosed in double quotes, otherwise the double quotes may be omitted.

Some modules also allow vectors of integers or floating point values as parameters. These have to be entered as strings, and since the values in these vectors are comma-separated, the strings must be enclosed in double quotes (e.g. ”0,1,2”). Vector types are marked by appending square brackets [] to the scalar type in the parameter description, similar to the notation used in languages such as C++.

Note that one parameter string will be used for any compression operation. This string contains parameters for all modules involved in the operation and each module extracts those parameters it understands and ignores all others. An example compression parameter could look like this (the keywords will be explained in Compression Algorithms): wavestr=zlib, zlevel=9

Compression format and parameters can be specified in the following ways:

1. Using rView: open the Prefs window and scroll to the bottom. Under Communication you will see list boxes for transfer and storage format and parameters. The transfer elements are used to determine the compression format and parameters for data transfer between rasdaman client and server (both ways), whereas the storage elements are used to determine the compression format and parameters for persistent storage in the database (i.e. only relevant when inserting data from rView). Enter the compression parameters as comma-separated strings in the appropriate text box (linefeeds are allowed) and activate them by pressing return or either the OK or Apply button.
2. Using the RasLib API: call your r_Database object’s set_transfer_format() or set_storage_format() method with the data format (defined in raslib/mddtypes.hh) and the parameter string after opening the database, depending on which you need.

By default, no compression is used for storage and transfer of MDD. Note that transfer and storage settings are activated on a per-client basis, so one client’s settings do not affect the other clients’ settings; that also means it isn’t possible to enable transfer compression for client B by enabling it via a helper client A that just opens the database, selects specific settings and then closes the database again.

4.24.4. Compression Algorithms

The rasdaman compression engine has a two-layer architecture as described in Compression Engine Architecture. The compression layer is represented by Compression Streams (see Compression Layer – Compression Streams); the various instances of the model layer (see Model Layers) use these compression streams to (de)compress the transformed tile data. In most cases the kind of compression stream to use can be configured via parameters to the model layer.

Compression Layer – Compression Streams and Model Layers describe the basic principles of the compression streams and model layers and are recommended reading to understand the compression engine in case you’re unfamiliar with the principles of compression algorithms. Concrete compression formats and their parameters are covered in Model Layer Overview and Parameters.

Model Layer

\(\longleftrightarrow\)

Section 4.2

Compression Layer

\(\longleftrightarrow\)

Section 4.1

Compression Layer – Compression Streams

The compression streams are normally not directly visible to the user, since they are used implicitly by the model layer and not standalone. It is important to describe them, however, to explain the behaviour of the higher layer of the compression engine. There are three types of compression streams available:

RLE:

(Run Length Encoding). This is a very simple (and therefore very fast) compression technique which collapses consecutive identical values and therefore works very well on sparse data, whereas it usually doesn’t achieve any compression at all on dense data. The main strength of RLE compression is speed, therefore it is very attractive for transfer compression.

ZLib:

This is the well-known standard compression library ZLib, which represents one of the best techniques for lossless compression of arbitrary data. It is a two-layer architecture in itself, with an LZ77 dictionary coder as model layer and Huffmann coding of the resulting dictionary coefficients as compression layer. LZ77 is an adaptive dictionary coding technique which finds repeating patterns in the data stream and replaces matches by a backwards reference into the data already processed and a length count. For example if the most recently processed sequence was abcbadcba and the remaining input starts with cbada, then cbad can be replaced by a backwards reference of -7 and a length count of 4, because the longest matching pattern appeared 7 characters earlier and is 4 characters long. Huffmann coding is entropy-based and represents frequent symbols by fewer bits than infrequent ones, thereby reducing the average number of bits used. ZLib compression usually performs very well and is often either the optimum or reasonably close to it. It has highly asymmetric complexity because of the LZ77 pattern searching phase, however, where compression can take more than 30 times as long as decompression in extreme cases. It is therefore only suitable for transfer compression if the bandwidth is very low or the data is already stored ZLib-compressed in the database and doesn’t have to be compressed before it can be transfered.

Arithmetic:

Arithmetic coding (AC) is the state-of-the-art entropy coding technique (superceding Huffmann coding (HC)). It represents a string of input symbols by a number in the unit interval; since the input string can have any length, the number in the unit interval can have very high precision. The main advantage of AC vs. HC is that AC can model any probability distribution exactly and can therefore – at least in theory – get arbitrarily close to the data’s entropy, whereas HC only reaches the entropy if the probabilities of all symbols are (negative) powers of 2. Another advantage is that adaptive AC can be implemented far more efficiently than adaptive HC (the AC in the rasdaman compression engine is also adaptive). Note that AC as a standalone compression technique (i.e. applied to untransformed data) almost always performs worse than ZLib, and frequently worse than RLE as well. AC is only recommended for highly decorrelated data like the output of the wavelet engine’s zerotree coder (for which it is also the default and outperforms all of its rivals).

Compression Layer Parameters

Currently only the ZLib compression stream supports a parameter for the rate vs. time tradeoff:

Keyword	Type	Default	Description
zlevel	integer	9	ZLib compression level between 0 (store only, fast) and 9 (best compression, slow)

Model Layers

A model layer is responsible for transforming the input data in such a way that the resulting data is no longer correlated. The transformed data is then fed into a compression stream, which should be able to achieve far better compression rates for this decorrelated data. The available model layers fall into three basic categories, ordered in increasing level of complexity:

None:

no transformation, feed the raw binary tile data with the default cell linearization order into the compression stream.

Channel separation:

compress each channel separately (see Compression Engine Architecture for a definition of channels). This model layer exploits the semantics of structured base types, which means it is equivalent to None if the MDD has an atomic base type.

Wavelet transformation:

process each channel separately and perform a multiresolution wavelet transformation on the channel data. Wavelet transformations perform spatial decorrelation by applying matching low-pass and high-pass filters to the data along all dimensions, thereby creating bands containing all possible combinations of average (low-pass response) and detail (high-pass response) coefficients for all dimensions (\(2^D\) bands, where \(D\) is the number of dimensions). We define the degree of detail of a band as the number of dimensions in which it holds detail information, so for instance a band with average coefficients in all dimensions has degree of detail 0, whereas a band with average coefficients in one dimension only has degree of detail 1 and so forth. The same procedure is then applied recursively to the band containing the average coefficients in all dimensions until a maximum number of resolution levels has been reached (either limited by the user (parameter mrlevels) or because the spatial extent of the low-pass response has become too small to allow further filtering). Consider the following examples:

2D:

(raster image) In the first step, the image with dimensions \(x \times y\) is transformed into four (\(= 2^2\)) bands with sizes \(\frac{x}{2} \times \frac{y}{2}\), where one of those bands is a scaled-down version of the original image (this band contains the average coefficients in both directions) and the other three contain the detail coefficients for three directions (horizontal, vertical, diagonal) which allow reconstructing the original image from the scaled-down version. The same algorithm is then applied recursively to the scaled-down version; a schematic diagram of this procedure can be seen in figure [FigureWaveExample].

Figure 4.26 This figure shows an example of the band decomposition resulting from multiresolution wavelet transformations. Each band has a name in {c,d}{c,d} with a resolution level number appended to it (decreasing for coarser levels). The number of the finest level is arbitrary and has no meaning in itself; in the examples it is always chosen such that resolution numbers don’t become negative for simplicity). c and d represent average (c) and detail (d) information in a given direction, where the first character represents horizontal and the second character vertical direction. The transformation starts with the original image (to the left) at the finest level \(3\) and decomposes this image into bands cc2, cd2, dc2 and dd3 (in the middle). The same transformations are then applied recursively to band cc2 (to the right) etc. until a coarsest level has been reached.

3D:

(tomogram) In the first step, the tomogram with dimensions \(x \times y \times z\) is transformed into eight (\(=2^3\)) bands with sizes \(\frac{x}{2} \times \frac{y}{2} \times \frac{z}{2}\), where the band containing the average coefficients in all three dimensions (ccc2) is again a scaled-down representation of the entire tomogram and the remaining 7 bands contain the detail information in the 7 directions possible for connecting a corner of a cube with the other corners (three along the edges, three diagonals on the faces, one diagonal through the cube, resulting in bands ccd2, cdc2, cdd2, dcc2, dcd2, ddc2 and ddd2). The same procedure is then applied recursively to the band containing only average coefficients along all directions.

Provided the data matches the wavelet filter, most of the detail coefficients will be very small and can be set to zero without noticeably affecting the quality of the reconstructed data (using the inverse wavelet transformation). That means that the detail coefficients are sparse and therefore highly compressible. Depending on whether the coefficients are stored with sufficient precision to allow reconstructing the original data exactly, wavelet compression techniques fall into two subclasses for lossless and lossy operation.

Any of these base categories can furthermore be combined with so-called predictors (see Predictor Overview and Parameters), an additional model layer which expresses a cell’s value as the difference of the actual cell value from an approximated value (using neighbouring cells to calculate the approximated value). Depending on where the neighbouring cells used for the prediction are located, predictors fall into two categories:

interchannel:

the neighbouring cells are in the other channels at the same position, so for instance in an RGB image the approximated value of the cell at position \(p\) in channel \(c\) could be calculated using the cells at position \(p\) in any set of channels \(\{c' : c' \ne c\}\). The rasdaman compression engine only allows one predicting channel \(c'\) for each predicted channel \(c\), however;

intrachannel:

the neighbouring cells are in the spatial neighbourhood of the same channel, so for instance the approximated value of the cell at position \(p\) in channel \(c\) could be calculated using the cells at positions \(p + z\) in channel \(c\) (where \(z\) is an offset vector or a set thereof).

Note: wavelet transformations can not be combined with intrachannel predictors because both do spatial decorrelation and would therefore compromise each other’s performance. Apart from this exception, the basic model layers and predictors are completely orthogonal concepts and can be combined arbitrarily.

Model Layer Overview and Parameters

In this section, the various data formats and their parameters will be explained. The names of the data formats will be given as listed in the rView Preferences window; programmers using the formats must include the raslib/mddtypes.hh header file and prefix this name by r_ (r + underscore). Note that a tile’s data format can change after updates, so creating an MDD where the tiles have a given data format \(X\) does not mean tiles will be stored in data format \(X\) on subsequent updates; the data format of new/modified tiles is the data format selected for the current update operation, not the format of the database tiles being updated.

All model layers allow enabling predictors using the following parameters (note: intrachannel prediction is not available for wavelets; predictors are described in more detail in Predictor Overview and Parameters):

Keyword	Type	Default	Description
predinter	string		Name of interchannel predictor (off by default). Possible names are delta and scaledelta, see Interchannel Predictors:
predintra	string		Name of intrachannel predictor (off by default; not available for wavelets). Possible names are hyperplane, neighbours and weighted, see Intrachannel Predictors:

The following model layers are currently available:

No Compression:

(data format Array) This is the default data format for tiles and disables compression entirely for these tiles. For local operation with high bandwidth this format usually performs best because there is no CPU overhead for (de)compression. For low bandwidths, e.g. over the internet, performance can be very bad, however, because in this case less time will be needed for (de)compression than for transferring the additional data volume caused by lack of compression.

No Transformation:

(data formats RLE, ZLib) In this format, the binary tile data is written directly into a compression stream without any previous transformation. The binary tile data is in default linearization order which hides spatial neighbourhoods in all dimensions but the last one (as a consequence of the default linearization order), and interleaves cell values. Consequently, there is no transformation overhead to speak of and the (de)compression speed of tiles in this format depends entirely on the speed of the underlying compression stream.

RLE works very well for sparse data (i.e. many consecutive identical values), where it is typically within 5%–10% of the compression rate of ZLib, but at a much higher speed. This makes RLE attractive for transfer compression (even over 10Mbit/s ethernet), in particular because it has only slightly asymmetric complexity for compression and decompression. On the downside, RLE achieves no compression at all for dense data.

ZLib is one of the most efficient standards for lossless compression and achieves very good compression rates (within the entropy limits) for most data types. It has highly asymmetric complexity for compression and decompression, however, which makes it unattractive for transfer compression where the compression overhead can easily exceed the savings in transfer time. Decompression is very fast, on the other hand, so in case data is read more often than written, it is very likely that overall system performance will improve if the tiles are stored in ZLib format in the database.

Channel separation:

(data formats SepRLE, SepZLib) In this format, the channels are compressed separately, but no spatial data neighbourhoods are exploited. Thus channel separation can often lead to better compression rates (compared to No Transformation) for MDD over structured base types such as RGB images; for MDD over atomic base types, these data formats are equivalent to the No Transformation ones. The underlying compression streams are the same as in the No Transformation case and the same comments apply. There is a small additional overhead caused by the channel separation, which is noticeably mostly in case of RLE compression (due to RLE’s speed), however.

Wavelet transformations:

wavelet transformations are based on filters with specifiv lengths and shape properties. The shape allows grouping the filters into families (such as Daubechies or Coiflet, see below) and the longer a filter, the better it usually is at analysing smooth data (i.e. less information is contained in the detail coefficients, making the detail bands sparser than shorter filters).

As far as processing complexity is concerned, wavelet transformations are very demanding and not recommended for transfer compression unless the bandwidth is particularily low. This is true in particular for lossy wavelets with zerotree quantization.

The order in which the wavelet bands (see figure [FigureWaveExample]) are processed when using lossless wavelets or bandwise homogeneous quantization is determined by a band iterator which groups detail bands into equivalence groups (identifying each group with an integer number) and iterates over these equivalence groups in sequence. This system is used to process bands consecutively which are expected to share similar properties, in order to optimize the performance of adaptive compression streams. Note that the type of the band iterator does usually not have a large influence on the compression of lossless wavelets but mostly on lossy wavelets because in this case it also groups bands into statistical units. For lossy wavelets, the use of bandwise homogeneous quantization is strongly discouraged, however, since the default zerotree quantization achieves much better compression rates and is also considerably easier to use. For all band iterators, the total average band is always in its own equivalence group 0, which is the first one processed. The following band iterator types are available:

isolevel:

bands on the same resolution level form an equivalence group. Iteration starts on the coarsest level and proceeds to the finer levels;

leveldet:

bands on the same resolution level and with the same degree of detail form an equivalence group. Iteration starts on the coarsest level with degree of detail 1 and increments first degree of detail until it has reached its maximum \(D\), then resets the degree of detail to 1 and proceeds to the next finer level;

isodetail:

bands with the same degree of detail form an equivalence group. Iteration starts with degree of detail 1 and iterates over all bands on all levels with this degree of detail, starting from the coarsest level. Then the degree of detail is incremented and the algorithm continues likewise.

All wavelet compression algorithms understand the following parameters:

Keyword	Type	Default	Description
wavestr	string	ZLib / Arith	A colon-separated list of compression stream(s) to use (e.g. RLE:Ari th would first RLE-code the data and send the output to an arithmetic coder. Possible stream names are RLE, ZLib and Arith (case is irrelevant). The default is a ZLib stream for everything but zerotree coding (lossy wavelets) and an adaptive arithmetic coder for zerotree coding
mrlevels	int	0	Maximum number of multiresolution levels to use for the wavelet transformation (compare with figure [FigureWaveExa mple]) . 0 means use the maximum number possible. Sometimes the numerical stability can be improved by reducing the number of resolution levels, in particular for low rates
banditer	string	leveldet	Possible values are isolevel (group by resolution level), leveldet (group by resolution level and degree of detail) and isodetail (group by degree of detail). The band iterator is ignored if zerotree coding is used

There are lossless and lossy wavelet classes available. Because wavelets perform by far the best if loss is acceptable, there is a strong bias on lossy compression in the wavelet classes.

• Lossless wavelets (data format HaarWavelet). There is currently only one lossless wavelet type, namely the Haar wavelet with a filter length of 2. Note that this filter is lossless for integer base types only, whereas loss in the general area of the machine precision can’t be avoided for floating point types. The performance of this filter depends largely on the MDD kind; in many cases ZLib or SepZLib with an appropriate intrachannel predictor perform better in both compression rate and time taken.

• Lossy wavelets (data formats QHaarWavelet (length 2), DaubechiesWavelet (length 4), DaubechiesNWavelet (\(N \in \lbrack 6, 20 \rbrack, N mod 2 = 0\)), LeastAsymNWavelet (\(N \in \lbrack 8, 20 \rbrack, N mod 2 = 0\)), CoifletNWavelet (\(N \in \lbrack 6, 30 \rbrack, N mod 6 = 0\))). In lossy wavelet compression, many of the orthogonal wavelet filters published in the standard literature are supported. The filters used belong to three basic families, the Daubechies family, the LeastAsymmetric family and the Coiflet family; numbers within the filter name describe the length of the filter, so Coiflet30Wavelet is a wavelet filter of the Coiflet family with a filter length of 30. As already mentioned above, longer filters are usually better at compressing smooth signals, at least for low-to-moderate rates (shorter filters tend to perform better on all kinds of MDD for high rates).

  Generic wavelet filters are floating point numbers, so applying such a filter to an MDD channel results in a floating point array of wavelet coefficients (i.e. a data expansion) which has to be quantized efficiently to achieve compression. There are two approaches possible here, bandwise homogeneous quantization (the older, simpler method) and generalized zerotree coding. In bandwise homogeneous quantization, the band iterator partitions the bands into equivalence groups and the quantizer assigns a constant number of bits per coefficient to each band equivalence group; the band data thus quantized is then fed into the compression stream. Generalized zerotree coding successively refines the approximation of the wavelet coefficients and achieves substantial compression by exploiting correlations between coefficients on neighbouring resolution levels. Zerotree coding almost always performs substantially better than bandwise homogeneous quantization in terms of compression rate and offers very simple control over the approximation quality, but it is also considerably more demanding on CPU power. Zerotree coding is the default quantization technique for lossy wavelets and using bandwise homogeneous quantization is discouraged.

  All lossy wavelets accept the following parameters:

  Keyword	Type	Default	Description
  wqtype	string	zerotree	The quantization technique, can be zerotree or perband
  enhancelv	integer	0	Enlarge the wavelet coefficients at the boundary of each band on the \(n\) finest levels (where \(n\) is the value of this parameter) before quantization (and reverse this operation after dequantization) to reduce boundary artifacts, in particular for low rates. This ensures that the boundary coefficients are encoded with more precision than the other coefficients.

  Most parameters of the compression engine deal with the quantization of wavelet coefficients for lossy wavelet compression. The following terms are important for bandwise homogeneous quantization:

  • relative number of bits means relative to the size of the base type of the original channel, i.e. quantizing an 8 bit channel with relative number of bits 0.5 means 4 bits per coefficient;
  • the band group number is determined by the band iterator (see the paragraph about band iterators above).

  The following compression parameters are available for bandwise homogeneous quantization:

  Keyword	Type	Default	Description
  qrtype	string	const	Set the relative number of bits to use per band group as a function. Possible values are: const (constant number of bits), linear (linearily decreasing with increasing group number), expnt (exponentially decreasing with increasing group number), gauss (squared-expone ntially decreasing with group number), custom (is implicitly activated by the relqbits parameter and can’t be selected directly)
  qntype	string	linear	Set the quantization technique, which can be linear (same resolution everywhere) and expnt (higher resolution around 0). If the data is highly concentrated around 0, the exponential quantizer can reduce the average quantization error
  bitscale	double	1	Scale factor for the curves defined by the qrtype parameter (except for custom)
  relqbits	double[]		Vector of doubles which specifies the relative number of bits for each band group, implicitly selects qrtype=custom The interpretation depends on the band iterator chosen
  cutoff	double	1	The number of the cutoff band group relative to the total number of band groups, starting from which band groups should be ignored entirely (i.e. quantized to 0)
  nullzone	double	0	Quantize all coefficients with an absolute value smaller than nullzone to 0

  As can be seen from these parameters, configuring bandwise homogeneous quantization is rather complicated and also dependent on external components like the band iterator. Zerotree coding is much easier to configure and offers much better control over the quantization fidelity.

  Remember the distortion measures defined in Compression Terminology which compared the original signal with the approximated signal. Similar to this, distortion measures \(Snr_w\), \(Psnr_w\) and \(Res_w\) can be defined which compare the original wavelet coefficients with the quantized (distorted) coefficients. Zerotree coding uses one of these three alternative distortion measures (selected by the user) as a termination criterion deciding when the coefficients have been encoded with sufficient precision and allows meeting that distortion threshold very closely. It is important to understand the difference between the distortion measures with and without the \(w\) index: with the \(w\) index they describe the distortion of the wavelet coefficients, without the \(w\) index they describe the distortion of the signal reconstructed from these coefficients. Both are loosely related, but the errors of the wavelet coefficients can be amplified in the reconstructed signal. Most importantly it is not possible to predict the distortion of the reconstructed signal from the distortion of the wavelet coefficients precisely enough to be practicable; you have to run tests to see how these two distortions are correlated for your data and the wavelet filter you intend to use.

  The following parameters apply to zerotree quantization (where \(Snr_w\) coding is the default and \(Snr_w\), \(Psnr_w\) and \(Res_w\) coding are mutually exclusive):

  Keyword	Type	Default	Description
  zttype	string	band1	Set the zerotree coding algorithm. Possible values are band1 (one-pass coding), band2 (two-pass coding with dominant and subordinate pass, corresponds to original zerotree coder)
  snr	double[]	\(10^4\)	Use \(SNR_w\) coding, terminating when the \(SNR_w\) of the wavelet coefficients is at least as large as this threshold value. The parameter is a vector of doubles because it is possible to specify different \(SNR_w\) values for each channel
  psnr	double[]	0	Use \(PSNR_w\) coding, otherwise like \(SNR_w\)
  residuum	double[]	0	Use \(RES_w\) coding, terminate when no approximated coefficient differs from its actual value by more than \(RES_w\)

  The difference between one-pass and two-pass coding is beyond the scope of this manual. Neither approach performs universally better than the other and neither is dramatically worse than the other in specific cases. The ideal coder must be determined experimentally for the user’s data and wavelet filter.

Predictor Overview and Parameters

Predictors are classified into intrachannel predictors and interchannel predictors, depending on whether they use cell values in spatially neighbouring cells or in neighbouring channels for prediction. Both types can be added to any of the model layers described above, with the exception of wavelet compression which does not support intrachannel prediction. Prediction first calculates an approximative value for a cell using neighbouring cells (neighbouring in either sense listed above) and then expresses this cell value as the difference (delta) of the actual value from the approximated value. The predictor processes the cells in such an order that the approximated values need not be stored explicitly but can be calculated by the inverse predictor from the cell values it already decoded, thus only the deltas have to be stored. If the predictor model matches the data well, most deltas will be concentrated around 0 and compress better than the untransformed values.

Interchannel Predictors:

Interchannel predictors approximate the value of a cell at position \(p\) in channel \(c\) by the value of a cell at the same position, but in a different channel \(c_p\). The values of channel \(c\) are then replaced by the difference to the predicted values, resulting in a delta channel. Provided the channels are correlated (as for instance often happens in colour images where brightness influences all three base colours), the value range of the delta channel will be smaller than that of the original channel, thereby allowing more efficient compression. All interchannel predictors require information about the \(c\!:\!c_p\) mappings, which is done by the following parameter:

Keyword	Type	Default	Description
intermap	string		Comma-separated list of channel mappings \(c\!:\!c_ p\) where \(c\) is the number of the channel being predicted and \(c_p\) is the predicting channel (channel numbers start from 0). Take care that no cyclic dependencies are allowed (such as 0:2,2:0)

There are currently two interchannel predictors available:

delta:

this predictor just uses the values of channel \(c_p\) directly as approximative values, for channel \(c\) which is recommended if channels are correlated and cover a similar value range, as e.g. often found in RGB images.

scaledelta:

this predictor first transforms the values of channel \(c_p\) such that they cover the same value range as those of channel \(c\) and uses the resulting values for prediction. This approach is recommended if the channels are correlated, but cover different value ranges (such as temperature and pressure in simulation data).

Intrachannel Predictors:

Intrachannel predictors approximate the value of a cell at position \(p\) in channel \(c\) by the values of cells at positions \(\{p + z_i\}\) where \(z_i\) are offset vectors describing the relative positions of all cells used for prediction (the predictor context). The available intrachannel predictors all calculate the approximated value as \(\frac{\sum_i w_i v(p + z_i)}{\sum_i w_i}\), where \(v(x)\) is the cell value at position \(x\) and \(w_i\) is the weight for the cell at offset \(z_i\) in the predictor context. The predicted cell’s value is then replaced by the difference to the approximated value and the iteration continues. As can be seen, intrachannel predictors write the deltas to the same channel they read the approximating values from, therefore care had to be taken to process cells in such an order that the inverse predictor can reconstruct the original data.

Currently there are three intrachannel predictors available:

hyperplane:

this predictor approximates a cell value by the value of the cell at offset \((-\delta_{0,k},\ldots,-\delta_{D-1,k})\), where \(D\) is the number of dimensions, \(k\) is the user-defined prediction direction (\(0 \le k < D\)) and \(\delta_{i,j}\) is the delta function which is \(1\) for \(i = j\) and \(0\) otherwise. For example in the 3D case, the predictor context can be the cell at offset \((-1,0,0)\) (\(k=0\)), the cell at offset \((0,-1,0)\) (\(k=1\)) or the cell at offset \((0,0,-1)\) (\(k=2\)). Thus neighbouring rows or columns will be used for prediction in a 2D MDD, neighbouring planes orthogonal to one axis in a 3D MDD and so forth. The value of \(k\) can be configured with the hypernorm parameter described below.

neighbours:

this predictor uses a subset of the cells whose position differs from that of the predicted cell by at most 1 in all dimensions for prediction. The set of all these cells has to be reduced to allow the inverse predictor to reconstruct the original data; for instance in the 2D case, the predictor context consists of the cells at offsets \((-1,-1)\), \((-1,0)\), \((-1,1)\) and \((0,-1)\) (an L-shaped set of cells). The approximating value is then calculated by using identical weights for all cells.

weighted:

this predictor uses the same predictor context, but different weights for diagonal cells. Each weight is initialized to 1 and then multiplied by a factor \(f\) for each dimension in which the position of the predicting cell differs from that of the one being predicted. For example in 2D, the cells at offsets \((-1,-1)\) and \((-1,1)\) would have weight \(f^2\) and the cells at offsets \((-1,0)\) and \((0,-1)\) would have weight \(f\). This technique allows reducing or enhancing the influence of diagonal cells on the approximated value, depending on the value of \(f\) which can be configured with the predweight parameter described below.

Some of these intrachannel predictors also allow configuration via compression parameters. The following parameters are currently available:

Keyword	Type	Default	Description
intralist	string	!	Comma-separated list of channel numbers to use the predictor on (starting from 0). The exclamation mark negates this list, so the default value ! means: apply the predictor to all channels
hypernorm	integer	0	Hyperplane prediction only: the number of the dimension orthogonal to the prediction hyperplane, i.e. the prediction direction (starting from 0)
predweight	double	0.5	Weighted neighbours prediction only: the amount a neighbouring cell’s weight is scaled by for every dimension where its coordinate differs from that of the predicted cell.

Other Parameters

In contrast to the compression parameters described so far, which are applicable to both storage and transfer compression, the following parameter is only relevant for transfer compression.

Keyword	Type	Default	Description
exactformat	integer	0	If exactformat =0, the transfer format will only be used by the server for transfer compression if the data was stored uncompressed in the database, otherwise the current compression format will be used. If exactformat =1, the server will always repack the data to the exact format requested by the client

Without this parameter it would be impossible to transfer an MDD to the client uncompressed that was stored compressed in the database. This problem may arise if there is a high bandwidth connection between server and client and the client has too little processing power for transparent decompression (or no decompression capabilities at all, such as the RasJ Java binding).

4.24.5. Examples

In the following examples, format: fmt means you have to use the data format fmt, params: str means you have to use the parameter string str and defaults: dstr means that additionally the default parameters described by dstr will be used implicitly. In rView, you can specify both by opening the preferences window and scrolling to the bottom, where configurations for storage and transfer compression can be found. If you use the C++ binding directly, you have to call your r_Database object’s set_transfer_format() or set_storage_format() method. For test purposes we recommend storing the test data uncompressed in the database and experimenting by changing transfer compression settings and loading the data to the client via lookups or queries. Once you’ve found satisfying data formats and/or parameters, you can copy the transfer compression configuration to the storage compression configuration and then store your test data in the database with these settings.

1. Compress using RLE:

   format:

   RLE

2. Compress using ZLib with the default compression level:

   format:	ZLib
   defaults:	zlevel=6

3. Compress using ZLib with a user-defined compression level (7):

   format:	ZLib
   params:	zlevel=7

4. Compress using RLE and the delta interchannel predictor, using channel 1 to predict channels 0 and 2:

   format:	RLE
   params:	predinter=delta, intermap="0:1,2:1"

5. Compress using ZLib and the hyperplane intrachannel predictor with the default prediction direction:

   format:	ZLib
   params:	predintra=hyperplane
   defaults:	zlevel=6, hypernorm=0

6. Compress using ZLib with the delta interchannel predictor predicting channel 0 by channel 1, and the hyperplane intrachannel predictor using the second dimension as user-defined prediction direction:

   format:	ZLib
   params:	predinter=delta, intermap="0:1" , predintra=hyperplane, hypernorm =1
   defaults:	zlevel=6

7. Compress using the lossless Haar wavelet with the default compression stream and band iterator:

   format:	HaarWavelet
   defaults:	wavestr=zlib, zlevel=9, banditer=leveldet, mrlevels=0

8. Compress using the lossless Haar wavelet with an RLE compression stream:

   format:	HaarWavelet
   params:	wavestr=rle
   defaults:	banditer=leveldet, mrlevels=0

9. Compress using the lossless Haar wavelet with a compression stream bank of ZLib followed by arithmetic coding and the delta interchannel predictor using channel 1 to predict channels 0 and 2:

   format:	HaarWavelet
   params:	wavestr="zlib:arith", predinter =delta, intermap="0:1,2:1", bandi ter=leveldet, mrlevels=0

10. Compress using the lossy Haar wavelet with the default quantization, the default zerotree type, the default termination criterion, an \(Snr_w\) of 100 for all channels and the default compression stream (arithmetic coder):

    format:	QHaarWavelet
    params:	snr=100
    defaults:	wqtype=zerotree, zttype=band1, wavestr=arith, enhancelv=0, mrlev els=0

11. Compress using the lossy Haar wavelet with two-pass zerotree quantization, \(Psnr_w\) coding with a \(Psnr_w\) of 300 for all channels and the default compression stream:

    format:	QHaarWavelet
    params:	zttype=band2, psnr=300
    defaults:	wqtype=zerotree, wavestr=arith, enhancelv=0, mrlevels=0

12. Compress using the lossy 4-tap Daubechies wavelet with the default quantization, the default zerotree type, \(Res\) coding with a maximum residual per cell of 0.1 for the first channel, 0.2 for the second channel and 0.3 for all other channels, and the default compression stream:

    format:	DaubechiesWavelet
    params:	res="0.1,0.2,0.3"
    defaults:	wqtype=zerotree, zttype=band1, wavestr=arith, enhancelv=0, mrlev els=0

13. Compress using the lossy 6-tap Coiflet wavelet with bandwise homogeneous quantization with the default quantizer, quantization, band iterator and compression stream:

    format:	Coiflet6Wavelet
    params:	wqtype=perband
    defaults:	qrtype=const, qntype=linear, bi tscale=1, cutoff=1, nullzone=0, b anditer=leveldet, wavestr=zlib, e nhancelv=0, mrlevels=0

14. Compress using the lossy 20-tap Daubechies wavelet with 3 multiresolution levels, bandwise homogeneous quantization with customized quantizer, exponential quantization, isolevel band iterator and RLE compression stream:

    format:	Daubechies20Wavelet
    params:	mrlevels=3, wqtype=perband, rel qbits="1, 0.75, 0.5, 0.25", qntyp e=expnt, banditer=isolevel, waves tr=rle
    defaults:	qrtype=custom, cutoff=1, nullzo ne=0, enhancelv=0

4.24.6. Hints & Tips

This section was written to provide some rules of thumb to reduce the vast amount of combinations possible with the compression engine to a manageable size depending on the kind of MDD that should be compressed. While it is not possible to a priori state an optimal compression technique for a given MDD, it is often possible to rule out several approaches entirely, which reduces the complexity of finding the optimal one considerably. Note, however, that all suggestions following below are heuristics and it is perfectly possible that they result in suboptimal compression for some MDD.

Hints for Lossless Compression

Lossless compression is easier to handle than lossy compression because it doesn’t require the user to specify a rate-distortion tradeoff since the distortion is always 0. Consequently there are only few model layers with a small set of parameters available for this type of compression; but combined with predictors, there are many combinations possible all the same.

• Use SepZLib or SepRLE rather than ZLib or RLE for multichannel data. Using SepZLib or SepRLE on data consisting of one channel only introduces some CPU overhead and basically identical compression rate (except for additional header meta data).
• The lossless Haar wavelet has in many cases inferior compression rate compared to ZLib with a suitable intrachannel predictor. Its use is therefore discouraged.
• ZLib is almost always the best compression stream for the lossless Haar wavelet.
• RLE and SepRLE only achieve compression on sparse data (many neighbouring cells have identical values, typically 0), on dense data they only introduce CPU overhead for compression but fail to reduce the data.
• On sparse data, the compression rates achievable with RLE and SepRLE are typically not far removed from those of ZLib and SepZLib, but RLE compression is far less demanding on the CPU and is therefore advantageous if speed is critical.

Hints for Lossy Compression

Lossy compression – which here always implies wavelet compression – represents the biggest and most complex part of the rasdaman compression engine. It is also the most complex to configure because it requires the user to set a tradeoff between rate and distortion via encoding quality parameters. While in many cases “lossy” algorithms can be made lossless by setting the encoding quality parameters to sufficiently high values, this is discouraged because the compression rate is almost always clearly inferior to that achieved by dedicated lossless compression techniques.

• Never use lossy compression for data transfer from client to server unless you fully understand the implications, not even if you want to store the data compressed in this format in the server. The server may have to retile and recompress the data, thereby performing another lossy compression of your data.
• Always use zerotree quantization with the adaptive arithmetic coder as compression stream (these are the defaults anyway). Bandwise homogeneous quantization is faster, but its compression rates are way inferior to those of zerotree quantization, in particular for low rates.
• Quality parameters: \(Snr_w\) coding models the inverse average distortion per cell, \(Psnr_w\) coding models the relative amplitude of the noise floor and \(Res_w\) coding models the maximum distortion per cell. So for instance if you want to make sure that no coefficient is encoded with a higher error than a given threshold value, use \(Res_w\) coding.
• The quality parameters concern the quantization of the wavelet coefficients and do not directly represent the distortion in the reconstructed data. Tests showed that typically the maximum error of the reconstructed data is by a factor of 2–3 larger than the maximum error of the wavelet coefficients, depending on the number of dimensions and the number of resolution levels.
• One-pass zerotree coding is often more efficient for predominantly dense data, whereas two-pass zerotree coding is more efficient for predominantly sparse data. For low rates, the differences between the two techniques are minute, however, and usually are quite small for high rates as well.
• Long filters (in excess of 8 taps) are usually only advantageous for smooth data and low quality. Many tests showed that for lossless or near lossless compression the Haar wavelet (2 taps) performed best. The Haar wavelet also has the fewest boundary artifacts.
• The biggest difference between filters in most tests was their length, not their family. so do not expect big differences in the performance of two 6-tap filters from different families.

Hints for Predictors

Predictors can often improve the compression rate considerably, but it is impossible to make definite statements about whether a specific predictor will achieve a positive effect for a given MDD; this must be determined by experiment.

interchannel predictors

(Interchannel Predictors:) are probably most attractive for multichannel raster images (RGB in the most popular case) where the channels often have substantial correlation (such as grey areas in RGB images). Use the delta predictor in these cases.

intrachannel predictors

(Intrachannel Predictors:) come in two complexities, low (hyperplane) and high (neighbours, weighted). While the predictor overhead per cell is constant for hyperplane, it increases with the number of dimensions for neighbours and weighted. Often hyperplane works better than its more complex counterparts, in particular if the data has a major correlation direction and hypernorm is set to that direction.

Hints for Transfer Compression

Transfer compression uses the fact that since a compressed object is smaller than its raw representation, it can be transferred over the communication channel faster. Unfortunately, the compression and decompression overhead may (and in many cases will) eat up the time saved by the smaller data size, so one can’t just use the compression algorithm that achieves the best compression rate without looking at the time it takes for compression and decompression as well. So whether a compression algorithm is suitable for transfer compression depends on the size \(s_c\) of the compressed data, the size \(s_r\) of the uncompressed data, the bandwidth \(B\) of the communication channel in bytes per second and the times \(t_c\) for compression and \(t_d\) for decompression. Using this terminology, it takes \(\frac{s_r}{B}\) seconds to transfer the uncompressed data and \(t_c + \frac{s_c}{B} + t_d\) when using transfer compression. That means transfer compression pays off if

\[\label{EquationTransferComp} t_c + \frac{s_c}{B} + t_d < \frac{s_r}{B} \Leftrightarrow t_c + t_d < \frac{s_r - s_c}{B},\]

which is the case if either (de)compression times or bandwidth are very low, or if space savings are very big. Any compression technique where the (de)compression times are higher than the transfer time of the uncompressed data (\(t_c + t_d \ge \frac{s_r}{B}\)) can be ruled out immediately, irrespective of the size of the compressed data.

There is also the special case where the data was already stored compressed in the database. In this case, tiles that don’t have to be trimmed can be sent directly to the client, so \(t_c = 0\), which is particularily attractive for compression algorithms with much higher complexity for compression than for decompression, most notably ZLib derivates.

Here are some rules of thumb for networks with different bandwidths, based on typical currently available CPU power:

100MBit Ethernet:

compression overhead outweighs space savings in practically all relevant cases.

10MBit Ethernet:

all wavelet variants can be ruled out due to their high (de)compression times. For sparse data, RLE and SepRLE can achieve a substantial reduction in overall transfer times. ZLib and SepZLib are usually too expensive for transfer compression, unless the data is stored compressed in this format in the database and consequently compression time is zero.

Modem connections:

tests showed that all compression algorithms process more than 100kB/s of raw data on a 400MHz Sun Enterprise server, so with typical modem bandwidths around 8–16kB/s, all compression algorithms have potential to improve overall transfer times.

Remember that the transfer format will be ignored for server \(\rightarrow\) client transfers if the exactformat parameter (cf. Other Parameters) is 0, the data was already stored compressed in the database and doesn’t have to be trimmed or processed otherwise – in this case the data will be transferred to the client in whatever format it was stored in.

4.24.7. Using the Compression Test Bed

The compression test bed is centered around the main compression utility test_compression. For lossy wavelet compression, there are some additional scripts to automate rate-distortion analysis and comparisons. If you have GNUPlot and a recent enough GhostScript installation on your system (must be able to create PDF files out of PS files), you can also automatically create all kinds of graphs out of the data measured.

The test_compression Utility

This utility allows testing all parts of the compression engine, using any kind of MDD for testing. To get an overview of the switches, type test_compression -h at the command line prompt.

There are three ways to specify test MDD to compress:

1. Synthetic (mostly for internal use): this very simple system allows you to create 2D MDD with any base type which are filled with a regular pattern. Use the -x and -y switches to specify the size of the test MDD and the -b switch to specify the base type (the format is the same as that used by rasdl, see the generic rasdaman documentation). The switch -c is just a shortcut for -b "struct { char, char, char }".
2. Files: this allows you to load the test data from a file. There are three different ways to interpret the file:
   • -r file: create a 1D MDD filled with the contents of file. Mostly for internal use.
   • -f file: load the TIFF image file and convert it into an MDD.
   • -i file: load a compressed MDD image from file (note that “image” is not meant in the graphical sense here). You must first create the image file using the -n switch, see the examples in test_compression Examples.
3. Database query: This allows you to connect to the rasdaman server and load a test MDD from there. Use the switches -s and -d to specify the rasserver you wish to contact and use either the -q switch followed by the actual query text or the -Q switch followed by the name of a file containing the query.

By default, test_compression compresses and decompresses the test MDD for the following compression types: Array, RLE, ZLib, SepRLE, SepZLib, HaarWavelet, DaubechiesWavelet, QHaarWavelet and Daubechies6Wavelet. If you add the switch -a, the test will be run on all compression types (essentially this includes all 22 wavelet filters). You can run the test for one specific compression type by using the switch -t comptype where comptype is the name of the compression type in the format displayed by test_compression -h (and case is irrelevant).

After compression, test_compression shows the absolute and relative size of the compressed data and writes the compressed MDD image to a file named data_comptype where comptype is the name of the compression type. After both compression and decompression have finished, test_compression compares the original data with the decompressed data and reports whether there are differences. In case there are differences, a small section of original and reconstructed data is written to the terminal, followed by an overview of data and error energy. The most important entries in this overview are \(Snr\), \(Psnr\) and maxdiff (= \(Res\)).

The switches -D and -l are for internal use only, since they are intended for benchmarking and require a special build of the compression library.

test_compression Examples

• Test the default MDD on HaarWavelet compression:

  test_compression -t haarwavelet
• Use the TIFF file test.tif as test MDD and compress it using ZLib compression with the hyperplane intrachannel predictor:

  test_compression -f test.tif -t zlib -p ’predintra=hyperplane’
• Create a portable (\(\rightarrow\) transparent endianness, -e switch below) compressed image file test.img from an MDD stored in collection testcoll in the database RASBASE on server testserver, and compress the image using ZLib compression:

  test_compression -s testserver -d RASBASE -e -n test.img -C -t zlib -q "SELECT x FROM testcoll AS x"
• Use the image file test.img created in the previous example and run DaubechiesWavelet compression on it with band2 zerotree quantization and an \(Snr\) of 1000:

  test_compression -i test.img -t daubechieswavelet -p ’zttype=band2, snr=1000’

The Scripts

Because it would be very tedious to run exhaustive rate-distortion analysis with just the test_compression utility – which is indispensable for serious evaluation of the engine – there are also some scripts to help automate the process. Using these scripts (and provided GNUPlot and GhostScript are installed on the system running the tests), it is possible to run the tests and create PDF diagrams with the results automatically.

In order for the scripts to work, all executables (such as test_compression and the scripts themselves) must reside in the directory $RMANBASE/compression/test whose location you can change via the value of the environment variable RMANBASE.

Several scripts accept data sources for test MDD using the -f file switch. Depending on the filename extension, file is interpreted as either a TIFF file (*.tif, *.TIF), a file containing a rasdaman query (*.ql, *.QL) or a compressed MDD image (otherwise).

Different kinds of rate-distortion data are identified by names in all scripts. Data measured is stored in files name.dat in a format suitable for GNUPlot, each containing two columns where the first is a position on the abscissa (\(x\)) and the second is a position on the ordinate (\(y\)). We will use the identifier \(q\) as a shortcut for the coding quality used (legal possibilities are zerotree coding with \(Snr_w\) or \(Psnr_w\) termination or bandwise homogeneous with the const quantizer, in which case \(q\) is the number of bits and only one-channel MDD may be used). The following name keys are defined:

relsize:

relative size of the compressed data in percent (\(x = q\), \(y = \mbox{relsize}\));

maxdiff:

maximum residual per cell of the reconstructed data (\(x = q\), \(y = Res\));

snr:

\(Snr\) of the reconstructed data (\(x = q\), \(y = Snr\));

psnr:

\(Psnr\) of the reconstructed data (\(x = q\), \(y = Psnr\));

rdmaxd:

relsize vs. max residual per cell of reconstructed data (\(x = \mbox{relsize}\), \(y = Res\));

rdsnr:

relsize vs. \(Snr\) of reconstructed data (\(x = \mbox{relsize}\), \(y = Snr\));

rdpsnr:

relsize vs. \(Psnr\) of reconstructed data (\(x = \mbox{relsize}\), \(y = Psnr\)).

These data files allow determining all parameters relevant for the compression of the test MDD with a given quality. If you wish to encode the MDD in such a way that the \(Snr\) is at least as large as a desired value \(S\), look up snr.dat, find the row where \(Snr\ge S\) (the second column) and use the quality parameter (first column) specified there. If you want to compress data to a relative size \(R\), look up relsize.dat, find the row with the closest relsize (second column) and use the quality parameter specified there (first column); the file rdsnr.dat shows you what \(Snr\) (second column) you get for this relsize (first column). Note that rdmaxd, rdsnr and rdpsnr are strictly speaking redundant, because they can be created by joining relsize with maxdiff, snr or psnr via the quality parameter \(q\) (and projecting \(q\) away); without tools to perform this join, it is much more convenient to just create this redundant data on the fly, however.

The data can also be processed into graphs using GNUPlot, via the scripts described below. The conventions here are that axes representing \(Snr\), \(Psnr\) and \(Res\) (for both wavelet coefficients and reconstructed data) are plotted logarithmically, whereas all other axes are plotted in the normal linear way.

ratedistort.sh

This script makes rate-distortion analysis for a user-specified test MDD, wavelet filter (default: DaubechiesWavelet) and quantization technique (default: one-pass zerotree). In all cases, there is an outer loop which increases the quality of the wavelet quantization after each iteration; in the loop body, the test MDD is compressed with the current quality settings, then decompressed and compared to the original MDD. Rate-distortion measurements are then written to the corresponding files (see the listing above for names and interpretations) within the directory rate-distort. For \(Snr_w\) and \(Psnr_w\) coding, the quality parameter is doubled after each iteration, for bandwise homogeneous coding the number of bits is incremented by one instead. The script stops if either the data could be reconstructed without loss or the maximum coding quality was reached. The following switches are available:

-f	source	specify data source for test MDD
-t	comptype	specify compression type (must be lossy wavelet)
-s	n	use \(SNR_w\) coding with an initial \(SNR_w\) of \(2^n\)
-p	n	use \(PSNR_w\) coding with an initial \(PSNR_w\) of \(2^n\)
-b	n	use bandwise homogeneous coding with an initial number of bits of n
-e	val	terminate the iteration once the coding quality has exceeded val
-o	params	parameter string params contains additional parameters
-r	server	specify rasdaman server name (for queries as data source)
-nb	bits	specify number of bits of the MDD’s cell base type for bandwise homogeneous coding

rateplot.sh

This script turns the rate-distortion data calculated by ratedistort.sh (cf. ratedistort.sh) into PDF graphs using GNUPlot to convert *.dat to *.ps and GhostScript to convert *.ps to *.pdf, so for each name.dat file, files name.gp, name.ps and name.pdf will be created (where by default all intermediate files are deleted, see switches -kgp and -kps below). Available switches are:

-d	dir	the *.dat files are in directory dir
-fname	name	use font name for regular text, default Times-Roman
-fsize	pts	size in points for the regular text, default 16
-cfname	name	use font name for captions, default Times-Bold
-cfsize	ptr	size in points for caption text, default 20
-kgp		don’t delete the GNUPlot scripts
-kps		don’t delete the PostScript files

all-test.sh

This script is the central component of the test bed and allows not only automating the use of scripts such as ratedistort.sh and rateplot.sh but also making cross-comparisons between the data measured for different wavelet types. Note that there are many options for internal use only, such as benchmarking, which will not be explained below. All data measured with this script is stored in the directory DATA (often in subdirectories of this directory) and all references to data files made in the remainder of this section are relative to this directory; a different one can be specified by using the -ddir switch. Doing automated rate-distortion analysis with all-test.sh means iterating over a set of wavelet and quantization types and calling ratedistort.sh and rateplot.sh for each. The resulting files are then stored in directories named datasource-quant-wavelet-rate, where

• datasource is the name of the source file without the extension (see -f switch below),
• quant is the quantization type which can be one of
  • snr (one-pass zerotree, \(Snr_w\) coding, arithmetic coder)
  • psnr (one-pass zerotree, \(Psnr_w\) coding, arithmetic coder)
  • snrz (one-pass zerotree, \(Snr_w\) coding, ZLib compression stream)
  • band (bandwise homogeneous coding, ZLib compression stream)
• wavelet is the name of the wavelet type (without the “Wavelet” postfix).

Thus, if the data source was the file vff_brain.img, possible directory names are vff_brain-snr-Daubechies-rate, vff_brain-snr-QHaar-rate, vff_brain-snrz-Coiflet6-rate etc. If you want to run the script for one specific value of quant only, use the -series switch with the name of one of the quantization types listed above. You can also append a postfix to the quantization name using the -wspost switch; this is convenient if you run the test for e.g. two-pass \(Snr_w\) zerotree coding, in which case you’d add -series snr -wspost 2 -o ’zttype=band2’ to the command line parameters of all-test.sh and get directories vff_brain-snr2-Daubechies-rate, vff_brain-snr2-QHaar-rate etc.

For all values of quant, the following wavelets are used (again omitting the “Wavelet” postfix): QHaar, Daubechies, Daubechies12 and Coiflet30. If quant equals snr, the following wavelets are used in addition: Daubechies6, Daubechies20, LeastAsym8, LeastAsym12, LeastAsym20, Coiflet6 and Coiflet18; otherwise Coiflet12 is added to the basic list.

A very important application of the all-test.sh script is to run comparisons over the data measured for different wavelets. This is done using the switches -cr or -call. The -cr switch needs the prefix of the directories to do rate-distortion comparisons over, which is the source file and quantization part of the directory name (prefix = datasource-quant); this scans for all directories named prefix-*-rate, creates rate-distortion comparisons for files rdfile.dat in these directories and saves the resulting data in the file prefix-compare-rdfile.pdf (as explained in the documentation of rateplot.sh, there are also intermediate files prefix-compare-rdfile.gp and prefix-compare-rdfile.ps which are normally deleted automatically, but can be preserved by adding the -kgp or -kps switch). Thus, possible names for comparison files are vff_brain-snr- compare-maxdiff.pdf, vff_brain-snr-compare-rdsnr.pdf, vff _brain-band-compare-snr.pdf etc. Alternatively you can compare specific directories only by using the -xcomp switch for all directories you wish to include in the comparison list (i.e. multiple -xcomp switches required). To further automate the process, the switch -call scans the DATA directory for all directories that can be identified as holding rate-distortion and performs cross-comparisons for all those with identical values for datasource and quant.

This description should allow you to comfortably run all necessary compression analysis. Here is a short overview over all the relevant switches covered in more detail above:

-h		show a short summary of all switches
-rd		run rate-distortion analysis; must be combined with suitable -f switch
-kgp		don’t delete the intermediate GNUPlot scripts
-kps		don’t delete the intermediate PostScript files
-call		make comparison graphs for all directories found
-ddir	dir	use dir as central data directory (default DATA)
-f	file	use file as data source file
-snr	n	use \(SNR_w\) coding and start with \(SNR_w = 2^n\)
-psnr	n	use \(PSNR_w\) coding and start with \(PSNR_w = 2^n\)
-qb	n	use bandwise homogeneous quantization, starting with \(n\) bits
-es	n	end \(SNR_w\) coding when \(SNR_w \ge 2^n\)
-ep	n	end \(PSNR_w\) coding when \(PSNR_w \ge 2^n\)
-eq	n	end bandwise homogeneous quantization with n bits per coefficient
-o	params	use parameter string params as additional parameters
-cr	prefix	make rate-distortion comparison graphs for directories named prefix-*-rate
-xcomp	dir	add the directory dir to the list of data directories to do rate-distortion comparisons over
-ras	srv	use srv as rasserver for queries
-nb	num	set the number of bits of the cell base type for bandwise homogeneous quantization to num
-series	quant	do measurements for quantization quant only
-wspost	str	append str to the quantization name in directory names
-prd	prefix	run rateplot.sh for all directories named prefix-*-rate
-pallrd		run rateplot.sh for all directories found

4.25. Access Control [RE]

This section covers the support for access control management in rasdaman.

Note

This is an experimental feature which is not yet generally available in the default rasdaman installation. To be enabled rasdaman must be started in experimental mode by adding export RASENGINE=1 at the beginning of /opt/rasdaman/bin/start_rasdaman.sh. Note, however, that this may break various queries in an unpredictable way.

4.25.1. Concepts

User

A client that connects to the rasdaman server must be identified by a user known by rasdaman. Each such user has:

• username - identifier ([a-zA-Z_][a-zA-Z0-9_]*)
• password - any string
• roles - a list of roles granted to the user

Further on we refer to the user with which a query is executed as current user.

Privilege

By default, users cannot do anything in the system. They need to be granted privileges (or permissions, rights): essentially shortcuts for a set of actions in the system.

Privileges can be:

1. Inclusive - allow performing certain operations (e.g. a SELECT query).
2. Exclusive - disallow performing certain operations. As users cannot do anything by default, this is used to fine-tune what is allowed by the inclusive privileges granted to the user. For example, a user may be allowed to do SELECT queries (1. above), but not over area [500:1000,200:430] of collection C.

Role

Roles allow to group privileges for easier management; they can be further granted to other roles or users.

Certain roles correspond to system-level privileges that cannot be modified by users, but can be granted/revoked as usual by users with the GRANT/REVOKE roles. These include:

Role	System privilege
read	SELECT
write	INSERT, UPDATE, DELETE, SELECT_INTO
info	DESCRIBE, LIST_TRIGGERS, LIST_USERS LIST_ROLES
admin	TYPE_MGMT, COLLECTION_MGMT, TRIGGER_MGMT, USER_MGMT, ROLE_MGMT, SERVER_MGMT, CONFIG_MGMT, GRANT, REVOKE

Note

At least one user on the system has to have the GRANT/REVOKE privileges; removing the last such user is not allowed.

Trigger

Triggers are special operations that are executed on each operation, so long as a few conditions are satisfied:

1. No exemption for this trigger has been granted to the user.
2. If BEFORE or AFTER is specified, the trigger is executed before the query evaluation starts, or afterwards.
3. The statement type matches the events if configured in the trigger (SELECT, INSERT, UPDATE, DELETE, etc).
4. Collections accessed in the query match any target collections specified in the trigger.
5. The boolean trigger condition expression evaluates to true.

The trigger action can be any rasql expression, most often an exception condition that denies authorization (exclusive privilege).

4.25.2. Syntax

User management

In general, performing any of the actions in this section requires the current user to have the USER_MGMT privilege.

Create a new user

CREATE USER u WITH PASSWORD "pw"

This will add a new user u with no priviliges in the system if it does not exist already.

The password is stored encrypted on the server and recovery is not possible if it is ever forgotten; in such a case it must be reset by another user with USER_MGMT privileges.

Change a user’s password

ALTER USER u SET PASSWORD TO "pw"   (1)
ALTER PASSWORD TO "pw"              (2)

(1) changes the password of a particular user u. The current user that invokes this query must have the USER_MGMT privilege only if it is different than the user u.

(2) will change the password of the current user with which the query is executed and does not require the current user to have USER_MGMT privileges.

Drop a user

DROP USER u

The above query completely deletes an existing user u from the system and removes it from any associated trigger exceptions and roles.

List all users

LIST USERS

Returns a comma-separated list of all users in the system (usernames in particular); executing this query requires LIST_USERS privileges.

Role management

In general, performing any of the actions in this section requires the current user to have the ROLE_MGMT privilege.

Create a new role

CREATE ROLE r

Similar to creating a user, this will add a new role r with no priviliges in the system if it does not exist already.

Drop a role

DROP ROLE r

The above query completely deletes an existing role r from the system and removes it from any associated trigger exceptions and roles.

List all roles

LIST ROLES

Returns a comma-separated list of all roles in the system; executing this query requires LIST_ROLES privileges.

Privilege management

Grant privileges

GRANT r TO r/u                      (1)
GRANT EXEMPTION FROM tr TO r/u      (2)

The GRANT statement allows assigning privileges to roles or users (1), or exemptions from trigger evaluation (2). As can be noticed, roles can be assigned to roles, which allows for building a flexible role hierarchy. Granting a previously granted privilege is ignored.

The current user must have GRANT privileges in order to perform these actions. With (1) only privileges that the current user itself has can be granted.

Revoke privileges

REVOKE r FROM r/u                   (1)
REVOKE EXEMPTION FROM tr TO r/u     (2)

The REVOKE statement supports the opposite action of removing privileges from roles or users (1), or trigger exemptions (2). Revoking a privilege that has not been granted is ignored.

The current user must have REVOKE privileges in order to perform these actions. With (1) only privileges that the current user itself has can be revoked.

List granted privileges

LIST ROLES FOR r/u                  (1)
LIST USERS WITH r                   (2)

Returns a comma-separated list of all roles granted to a role r or user u (1), or users which have a role r granted (2) in the system.

Executing (1) requires LIST_ROLES privileges, while (2) requires LIST_USERS privileges.

Trigger management

In general, performing the actions in this section requires the current user to have the TRIGGER_MGMT privilege.

Create a trigger

CREATE TRIGGER tr
[ SELECT | INSERT | UPDATE | DELETE ] -- not supported yet
[ ON coll1, coll2, ... ]              -- not supported yet
WHEN conditionExp
BEGIN actionExp END

The statement above allows to create a trigger named tr. The trigger subsequently runs on matching queries, as long as the current user does not have an explicit exemption (see Privilege management).

Trigger Condition

The conditionExp must result in a scalar boolean value: if true, the actionExp is evaluated. Specific operations can be used as a conditionExp to allow testing whether elements of a collection (optionally in a specific area) would be accessed or modified by a query.

accessed( coll [ , sdom ] )
modified( coll [ , sdom ] )

These two operations return a boolean array of the specified sdom, or the sdom of the whole input array if not specified. Any operations applicable on boolean arrays can be applied on the result, including:

• some_cells, all_cells, count_cells
• and, or, not

In addition, a special context object is available in the condition expression, with several useful attributes (accessible via the dot . operator).

Context attribute	Description
ACCESSVOLUME, ESTIMATEDACCESSVOLUME	Data volume (in bytes) accessed from disk during the query execution.
TRANSFERVOLUME, ESTIMATEDTRANSFERVOLUME	Data volume (in bytes) transferred between federated nodes during query execution. Not yet supported.
RESULTVOLUME, ESTIMATEDRESULTVOLUME	Data volume (in bytes) that will be returned to the user at the end of query execution.
TIME, ESTIMATEDTIME	Time (in seconds) to execute the query.
CYCLES, ESTIMATEDCYCLES	CPU cycles to execute the query.
MEMORY, ESTIMATEDMEMORY	Main memory used to execute the query.
USERNAME, PASSWORD	User credentials.
QUERY	The query string to be executed.
STARTTIME	The time at which query execution started.

The estimated values are calculated before the query execution starts, so they may not be precise; their counterparts are calculated after the query finishes execution and are 100% correct. ESTIMATEDACCESSVOLUME is an exception as it can actually be precisely determined before the query executes.

Currently the following attributes are not yet supported: ESTIMATEDTIME, ESTIMATEDCYCLES, ESTIMATEDMEMORY, TRANSFERVOLUME / ESTIMATEDTRANSFERVOLUME.

Trigger Action

In the actionExp an exception operator is allowed, which would terminate evaluation with the specified exception error text.

EXCEPTION "error text"

Drop a trigger

DROP TRIGGER tr

The above query completely deletes an existing trigger tr from the system and removes it any trigger exemptions associated with it.

List triggers

LIST TRIGGER tr                     (1)
LIST TRIGGERS                       (2)

(1) returns the CREATE TRIGGER statement for trigger tr, while (2) returns a comma-separated list of all triggers in the system.

Executing either query requires LIST_TRIGGERS privileges.

Examples

“Restrict access to top-secret area on all users”

CREATE TRIGGER top_secret_area_trigger
WHEN some_cells( accessed( mr2, [0:50,100:150] ) )
BEGIN
  EXCEPTION "Access denied to top-secret area."
END

“Grant exemption to user rasadmin”

GRANT EXEMPTION FROM top_secret_area_trigger TO rasadmin

By default the trigger will deny any access on mr2 intersecting with the subset [0:50,100:150] to any system user, including admins. The query above gives an exemption to the rasadmin user, so that it is allowed to access this area.

“Prevent users from accessing more than 100 MB”

CREATE TRIGGER max_data_access_trigger
WHEN CONTEXT.ACCESSVOLUME > 100000000
BEGIN
  EXCEPTION "Data access is restricted to 100 MB."
END

“Prevent users from retrieving more than 100 MB”

CREATE TRIGGER max_data_result_trigger
WHEN CONTEXT.RESULTVOLUME > 100000000
BEGIN
  EXCEPTION "Data download is restricted to 100 MB."
END

“Drop triggers”

After testing around the triggers, do not forget to drop them in order to avoid problems with trying other examples in the Query Language Guide.

DROP TRIGGER top_secret_area_trigger
DROP TRIGGER max_data_access_trigger
DROP TRIGGER max_data_result_trigger

4.26. Web Access to rasql

4.26.1. Overview

As part of petascope, the geo service frontend to rasdaman, Web access to rasql is provided. The request format is described in Request Format, the response format in Response Format below.

4.26.2. Service Endpoint

The service endpoint for rasql queries is

http://{service}/{path}/rasdaman/rasql

4.26.3. Request Format

A request is sent as an http GET URL with the query as key-value pair parameter. By default, the rasdaman login is taken from the petascope settings in petascope.properties; optionally, another valid rasdaman user name and password can be provided as additional parameters.

Syntax

http://{service}/{path}/rasdaman/rasql?params

This servlet endpoint accepts KVP requests with the following parameters:

query=q

where q is a valid rasql query, appropriately escaped as per http specification.

username=u

where u is the user name for logging into rasdaman (optional, default: value of variable rasdaman_user in petascope.properties)

password=p

where p is the password for logging into rasdaman (optional, default: value of variable rasdaman_pass in petascope.properties)

Example

The following URL sends a query request to a fictitious server www.acme.com:

http://www.acme.com/rasdaman?
    query=select%20rgb.red+rgb.green%20from%20rgb
    &username=rasguest
    &password=rasguest

4.26.4. Response Format

The response to a rasdaman query gets wrapped into a http message. The response format is as follows, depending on the nature of the result:

If the query returns arrays, then the MIME type of the response is application/octet-stream.

• If the result is empty, the document will be empty.
• If the result consists of one array object, then this object will be delivered as is.
• If the result consists of several array objects, then the response will consist of a Multipart/MIME document.
• If the query returns scalars, all scalars will be delivered in one document of MIME type text/plain, separated by whitespace.

4.26.5. Security

User and password are expected in cleartext, so do not use this tool in security sensitive contexts.

The service endpoint rasdaman/rasql, being part of the petascope servlet, can be disabled in the servlet container’s setup (such as Tomcat).

4.26.6. Limitations

Currently, no uploading of data to the server is supported. Hence, functionality is restricted to queries without positional parameters $1, $2, etc.

Currently, array responses returned invariably have the same MIME type, application/octet-stream. In future it is foreseen to adjust the MIME type to the identifier of the specific file format as chosen in the encode() function.

4.27. Appendix A: rasdl Grammar

This appendix presents a simplified list of the main rasdl grammar rules used in the rasdaman system. The grammar is described as a set of production rules. Each rule consists of a non-terminal on the left-hand side of the colon operator and a list of symbol names on the right-hand side. The vertical bar | introduces a rule with the same left-hand side as the previous one. It is usually read as or. Symbol names can either be non-terminals or terminals (the former ones printed in bold face as a link which can be followed to the non-terminal production). Terminals represent keywords of the language, or identifiers, or number literals; “(“, “)”, “[“, and “]” are also terminals, but they are in double quotes to distinguish them from the grammar parentheses (used to group alternatives) or brackets (used to indicate optional parts).

typeDef        ::=   structDef
                   | marrayDef
                   | setDef
structDef      ::=  struct structName "{" attrList "}"
structName     ::=  identifier
attrList       ::=   attrType attrName
                     [ ; attrList ]
attrType       ::=  identifier
attrName       ::=  identifier
marrayDef      ::=   typedef
                     marray < typeName
                              [ , spatialDomain ] >
                     marrayName
spatialDomain  ::=  "[" spatialExpList "]"
spatialExpList ::=  spatialExp [ , spatialExpList ]
spatialExp     ::=  integerExp | intervalExp
setDef         ::=  typedef set < marrayName > setName
                    [ nullExp ]
setName        ::=  identifier
marrayName     ::=  identifier

4.28. Appendix B: rasql Grammar

This appendix presents a simplified list of the main rasql grammar rules used in the rasdaman system. The grammar is described as a set of production rules. Each rule consists of a non-terminal on the left-hand side of the colon operator and a list of symbol names on the right-hand side. The vertical bar | introduces a rule with the same left-hand side as the previous one. It is usually read as or. Symbol names can either be non-terminals or terminals (the former ones printed in bold face as a link which can be followed to the non-terminal production). Terminals represent keywords of the language, or identifiers, or number literals; “(“, “)”, “[“, and “]” are also terminals, but they are in double quotes to distinguish them from the grammar parentheses (used to group alternatives) or brackets (used to indicate optional parts).

query               ::=   createExp
                        | dropExp
                        | selectExp
                        | updateExp
                        | insertExp
                        | deleteExp
createExp           ::=   createCollExp
                        | createStructTypeExp
                        | createMarrayTypeExp
                        | createSetTypeExp
createCollExp       ::=  create collection
                         namedCollection typeName
createCellTypeExp   ::=  create type typeName
                         a" cellTypeExp
cellTypeExp         ::=  "(" attributeName typeName
                             [ , attributeName typeName ]... ")"
createMarrayTypeExp ::=  create type typeName
                         as "(" cellTypeExp | typeName ")"
                         mdarray domainSpec
domainSpec          ::=  "[" extentExpList "]"
extentExpList       ::=   extentExp [ , extentExpList ]
extentExp           ::=  axisName
                         [ "(" integerLit | intervalExp ")" ]
boundSpec           ::=  integerExp
createSetTypeExp    ::=  create type typeName
                         as set "(" typeName ")"
                         "[" nullExp "]"
nullExp             ::=  null values mintervalExp
dropExp             ::=   drop collection namedCollection
                        | drop type typeName

selectExp         ::=   select resultList
                        from collectionList
                        [ where generalExp ]
updateExp         ::=  update iteratedCollection
                       set updateSpec
                       assign generalExp
                       [ where generalExp ]
insertExp         ::=  insert into namedCollection
                       values generalExp
                       [ tiling [ StorageDirectives ] ]
StorageDirectives ::=   RegularT | AlignedT | DirT
                      | AoiT | StatT
RegularT          ::=  regular TileConf
                       [ tile size integerLit ]
AlignedT          ::=  aligned TileConf [ TileSize ]
DirT              ::=  directional SplitList
                       [ with subtiling [ TileSize ] ]
AoiT              ::=  area of interest BboxList
                       [ TileSize ]
StatT             ::=  statistic TileConf [ TileSize ]
                       [ border threshold integerLit ]
                       [ interest threshold floatLit ]
TileSize          ::=  tile size integerLit
TileConf          ::=  BboxList [ , BboxList ]...
BboxList          ::=  "[" integerLit : integerLit
                           [ , integerLit : integerLit ]... "]"
Index             ::=  index IndexName
deleteExp         ::=  delete from iteratedCollection
                       [ where generalExp ]
updateSpec        ::=  variable [ mintervalExp ]
resultList        ::=  [ resultList , ] generalExp

generalExp         ::=   mddExp
                       | trimExp
                       | reduceExp
                       | inductionExp
                       | caseExp
                       | functionExp
                       | integerExp
                       | condenseExp
                       | variable
                       | mintervalExp
                       | intervalExp
                       | generalLit
mintervalExp       ::=   "[" spatialOpList "]"
                       | sdom "(" collIterator ")"
intervalExp        ::=  ( integerExp | * ) :
                        ( integerExp | * )
integerExp         ::=   integerTerm + integerExp
                       | integerTerm - integerExp
                       | integerTerm
integerTerm        ::=   integerFactor * integerTerm
                       | integerFactor / integerTerm
                       | integerFactor
integerFactor      ::=   integerLit
                       | identifier [ structSelection ]
                       | mintervalExp . lo
                       | mintervalExp . hi
                       | "(" integerExp ")"
spatialOpList      ::=  spatialOpList2
spatialOpList2     ::=   spatialOpList2 , spatialOp
                       | spatialOp
spatialOp          ::=  generalExp
condenseExp        ::=  condense condenseOpLit
                        over condenseVariable in generalExp
                        [ where generalExp ]
                        using generalExp
condenseOpLit      ::=  + | * | and | or | max | min
functionExp        ::=   version "(" ")"
                       | unaryFun "(" collIterator ")"
                       | binaryFun
                         "(" generalExp , generalExp ")"
                       | transcodeExp
unaryFun           ::=  oid | dbinfo
binaryFun          ::=  shift | scale | bit | pow | power | div | mod
transcodeExp       ::=   encode "(" generalExp , StringLit
                                      [ , StringLit ] ")"
                       | decode "(" $ integerLit
                                     [ , StringLit
                                       , StringLit ] ")"
                       | decode "(" generalExp ")"
structSelection    ::=  . ( attributeName | integerLitExp )
inductionExp       ::=   unaryInductionOp "(" generalExp ")"
                       | generalExp . ( re | im )
                       | generalExp structSelection
                       | not generalExp
                       | generalExp binaryInductionOp generalExp
                       | ( + | - ) generalExp
                       | "(" castType ")" generalExp
                       | "(" generalExp ")"
unaryInductionOp   ::=   sqrt | abs | exp | log | ln
                       | sin | cos | tan | sinh | cosh
                       | tanh | arcsin | arccos | arctan
binaryInductionOp  ::=   overlay | is | = | and | or
                       | xor | plus | minus | mult
                       | div| equal | < | > | <=
                       | >= | !=
castType           ::=   bool | char | octet | short
                       | long | ulong | float | double
                       | ushort | unsigned ( short | long )
caseExp            ::=  case [ generalExp ] whenList
                        else generalExp end
whenList           ::=  [ whenList ]
                        when generalExp
                        then generalExp
collectionList     ::=  [ collectionList , ]
                        iteratedCollection
iteratedCollection ::=  namedCollection
                        [ [ as ] collIterator ]
reduceExp          ::=  reduceIdent "(" generalExp ")"
reduceIdent        ::=   all_cells | some_cells | count_cells
                       | avg_cells | min_cells | max_cells
                       | add_cells
                       | stddev_samp | stddev_pop
                       | var_samp | var_pop
trimExp            ::=  generalExp mintervalExp
mddExp             ::=  marray ivList values generalExp
ivList             ::=  [ ivList , ]
                        marrayVariable in generalExp
generalLit         ::=  scalarLit | mddLit | StringLit | oidLit
oidLit             ::=  < StringLit >
mddLit             ::=   < mintervalExp dimensionLitList >
                       | $ integerLit
dimensionLitList   ::=  [ dimensionLitList ; ] scalarLitList
scalarLitList      ::=  [ scalarLitList , ] scalarLit
scalarLit          ::=  complexLit | atomicLit
complexLit         ::=  [ struct ] { scalarLitList }
atomicLit          ::=   booleanLit | integerLit | floatLit
                       | complex "(" floatLit , floatLit ")"
typeName           ::=  identifier
variable           ::=  identifier
namedCollection    ::=  identifier
collIterator       ::=  identifier
attributeName      ::=  identifier
marrayVariable     ::=  identifier
condenseVariable   ::=  identifier
identifier         ::=  [a-zA-Z_] [a-zA-Z0-9_]*

[1]	Actually, rasdl is a subset of ODMG’s Object Definition Language (ODL) with the only extension for spatial domain specification within the array template.

[2]	memory usage is one byte per pixel

[3]	dependent on the relational base DBMS used; please consult the External Products Integration Guide for your environment.

[4]	Currently only one -f argument is supported (i.e., only $1).

[5]	the dimension which is the leftmost in the spatial domain specification

[6]	the dimension which is the rightmost in the spatial domain specification

[7]	Null means a numerical value of 0 (zero).

[13]	This is going to be changed in the near future.

[14]	This will be changed in future.

[15]	This is referred to as Strict 2-Phase Locking in databases.